
【题目】如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为 . 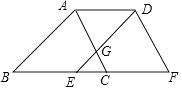
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,AB=13,AC=12,以B为圆心,5为半径的圆与直线AC的位置关系是( )
A. 相切B. 相交C. 相离D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=2x,下列结论中正确的是( )
A. 函数图象都经过点(2,1) B. 函数图象都经过第二、四象限
C. y随x的增大而增大 D. 不论x取何值,总有y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程.在括号内的横线上填空或填上推理依据.
如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD
证明:∵AB∥EF
∴∠APE=()
∵EP⊥EQ
∴∠PEQ=()
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥()
∴AB∥CD()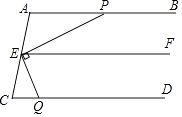
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(Ⅰ)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(Ⅱ)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
(Ⅲ)现需按毛利润的10%交纳各种税费,人工费每日按销售量每千克支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每千克涨价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( ) 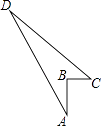
A.6cm2
B.30cm2
C.24cm2
D.36cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数y=kx-1(k≠0)在第一象限的图象交于A(1,n)和B两点.
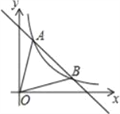
(1)求反比例函数的解析式与点B坐标;
(2)求△AOB的面积;
(3)在第一象限内,当一次函数y=﹣x+5的值小于反比例函数y=kx-1(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com