
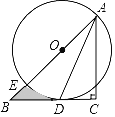
【题目】如图,在![]() 中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.
中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.
(1)连结AD,求证:AD平分∠CAB;
(2)若BE=![]() ﹣1,求阴影部分的面积.
﹣1,求阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,证OD∥AC,求出∠OAD=∠ODA=∠CAD即可;
(2)证明△BOD是等腰直角三角形,分别求出△BOD和扇形EOD的面积即可.
(1)证明:如图,连结OD,
∵⊙O与BC相切于点D,
∴OD⊥BC,
即∠ODB=90°.
又∵∠C=90°,
∴OD∥AC,
∴∠ODA=∠CAD.
在⊙O中,OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,
∴AD平分∠CAB.
(2)解:在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=45°,
∴∠BOD=45°,
∴△BOD是等腰直角三角形,
∴OB=![]() OD,BD=OD,
OD,BD=OD,
设⊙O的半径为r,则OD=BD=r,![]() ,
,
∴![]() ,
,
∴r=1,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
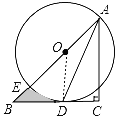
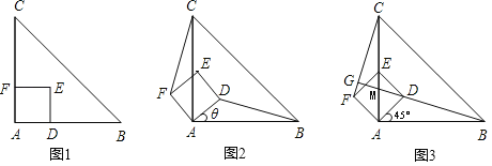
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G, AC与BG的交点为M.求证:EM:DM=CG:AC;
(3)在(2)小题的条件下,当AB=4,AD=![]() 时,求四边形ABGF的面积.
时,求四边形ABGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
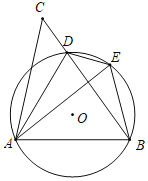
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.
(1)求证:AE=AB.
(2)填空:
①当∠CAB=90°,cos∠ADB=![]() ,BE=2时,边BC的长为 .
,BE=2时,边BC的长为 .
②当∠BAE= 时,四边形AOED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 是
是![]() 右侧半圆上的一个动点,点
右侧半圆上的一个动点,点![]() 是
是![]() 左侧半圆的中点,
左侧半圆的中点,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,
,![]()
![]() ,
,![]() .
.
(1)当![]() 时, 求证:
时, 求证:![]() .
.
(2)若![]() 的半径为
的半径为![]() ,请填空:
,请填空:
①当四边形![]() 为正方形时,
为正方形时,![]()
②当![]() 时, 四边形
时, 四边形![]() 为菱形.
为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(要求保留作图痕迹,不写作法)

(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);
(2)连结BE,若AC=10,AB=6,求△ABE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
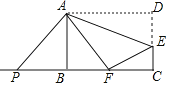
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( )
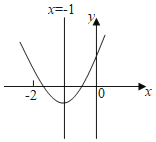
A.b2>4acB.abc>0
C.a﹣c<0D.am2+bm≥a﹣b(m为任意实数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
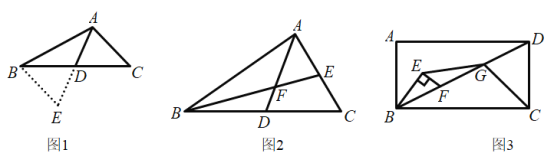
小红遇到这样一个问题:如图1,![]() 中,
中,![]() ,
,![]() ,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使
,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使![]() ,连接BE,证明
,连接BE,证明![]() ,经过推理和计算使问题得到解决.
,经过推理和计算使问题得到解决.
请回答:(1)小红证明![]() 的判定定理是:__________________________________________;
的判定定理是:__________________________________________;
(2)AD的取值范围是________________________;
方法运用:
(3)如图2,AD是![]() 的中线,在AD上取一点F,连结BF并延长交AC于点E,使
的中线,在AD上取一点F,连结BF并延长交AC于点E,使![]() ,求证:
,求证:![]() .
.
(4)如图3,在矩形ABCD中,![]() ,在BD上取一点F,以BF为斜边作
,在BD上取一点F,以BF为斜边作![]() ,且
,且![]() ,点G是DF的中点,连接EG,CG,求证:
,点G是DF的中点,连接EG,CG,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式![]() 的几何意义是数轴上
的几何意义是数轴上![]() 所对应的点与2所对应的点之间的距离;因为
所对应的点与2所对应的点之间的距离;因为![]() ,所以
,所以![]() 的几何意义就是数轴上
的几何意义就是数轴上![]() 所对应的点与
所对应的点与![]() 所对应的点之间的距离.
所对应的点之间的距离.
⑴. 发现问题:代数式![]() 的最小值是多少?
的最小值是多少?
⑵. 探究问题:如图,点![]() 分别表示的是
分别表示的是![]() ,
,![]() .
.
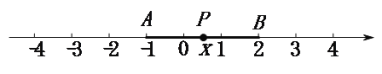
∵![]() 的几何意义是线段
的几何意义是线段![]() 与
与![]() 的长度之和
的长度之和
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点点
;当点点![]() 在点
在点![]() 的左侧或点
的左侧或点![]() 的右侧时
的右侧时 ![]()
∴![]() 的最小值是3.
的最小值是3.
⑶.解决问题:
①.![]() 的最小值是 ;
的最小值是 ;
②.利用上述思想方法解不等式:![]()
![]()
③.当![]() 为何值时,代数式
为何值时,代数式![]() 的最小值是2.
的最小值是2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com