
����Ŀ���ҹ�������ѧ�һ���˵������ȱ��ʱ��ֱ�ۣ�������ʱ�����������ν���ǽ����ѧ�������Ҫ˼�뷽��.���磬����ʽ![]() �ļ���������������
�ļ���������������![]() ����Ӧ�ĵ���2����Ӧ�ĵ�֮��ľ��룻��Ϊ
����Ӧ�ĵ���2����Ӧ�ĵ�֮��ľ��룻��Ϊ![]() ������
������![]() �ļ����������������
�ļ����������������![]() ����Ӧ�ĵ���
����Ӧ�ĵ���![]() ����Ӧ�ĵ�֮��ľ�����
����Ӧ�ĵ�֮��ľ�����
��. �������⣺����ʽ![]() ����Сֵ�Ƕ��٣�
����Сֵ�Ƕ��٣�
��. ̽�����⣺��ͼ����![]() �ֱ��ʾ����
�ֱ��ʾ����![]() ��
��![]() ��
��
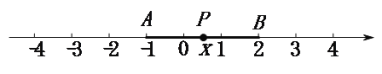
��![]() �ļ����������߶�
�ļ����������߶�![]() ��
��![]() �ij���֮��
�ij���֮��
�൱��![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��![]() ;�����
;�����![]() �ڵ�
�ڵ�![]() �������
�������![]() ���Ҳ�ʱ
���Ҳ�ʱ ![]()
��![]() ����Сֵ��3��
����Сֵ��3��
��.������⣺
��.![]() ����Сֵ�� ��
����Сֵ�� ��
��.��������˼�뷽���ⲻ��ʽ��![]()
![]()
��.��![]() Ϊ��ֵʱ������ʽ
Ϊ��ֵʱ������ʽ![]() ����Сֵ��2��
����Сֵ��2��
���𰸡���6����![]() ��
��![]() ����
����![]() ��
��![]()
��������
(3)�ٸ��ݾ���ֵ�ļ��������֪����������ϵĵ㵽-2�ľ���͵�4�ľ���֮�͵���Сֵ��
�ڸ������⻭����Ӧ��ͼ�Σ�ȷ��������ʽ�Ľ⼯���ɣ�
�۸���ԭʽ����СֵΪ2���õ�3��ߺ��ұߣ��ҵ�3����Ϊ2�ĵ㼴�ɣ�
�⣺(3)����A��ʾ����Ϊ4��B��ʾ����Ϊ-2��P��ʾ����Ϊx��
��![]() ��ʾ�����ϵĵ�P��4�ľ��룬���߶�PA��ʾ��
��ʾ�����ϵĵ�P��4�ľ��룬���߶�PA��ʾ��
![]() ��ʾ�����ϵĵ�P��-2�ľ��룬���߶�PB��ʾ��
��ʾ�����ϵĵ�P��-2�ľ��룬���߶�PB��ʾ��
��![]() �ļ��������ʾΪPA+PB����P���߶�AB��ʱȡ����СֵΪAB��
�ļ��������ʾΪPA+PB����P���߶�AB��ʱȡ����СֵΪAB��
���߶�AB�ij���Ϊ6��
��![]() ����СֵΪ6.
����СֵΪ6.
�ʴ�Ϊ��6.
����A��ʾ-3��B��ʾ1��P��ʾx��
���߶�AB�ij���Ϊ4����
![]() �ļ��������ʾΪPA+PB��
�ļ��������ʾΪPA+PB��
������ʽ�ļ���������PA+PB��AB��
��P�������߶�AB�ϣ�Ӧ����A��������B���Ҳ࣬
������ʽ�Ľ⼯Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
����A��ʾ-a��B��ʾ3��P��ʾx��
���߶�AB�ij���Ϊ![]() ��
��
![]() �ļ��������ʾΪPA+PB����P���߶�AB��ʱPA+PBȡ����Сֵ��
�ļ��������ʾΪPA+PB����P���߶�AB��ʱPA+PBȡ����Сֵ��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
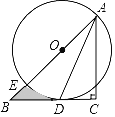
����Ŀ����ͼ����![]() �У���C=90����AC=BC����O��AB�ϣ���OΪԲ�ģ�OAΪ�뾶����O����BC�����ڵ�D���ҽ�AB�ڵ�E��
�У���C=90����AC=BC����O��AB�ϣ���OΪԲ�ģ�OAΪ�뾶����O����BC�����ڵ�D���ҽ�AB�ڵ�E��
��1������AD����֤��ADƽ�֡�CAB��
��2����BE=![]() ��1������Ӱ���ֵ������
��1������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ӿ����ͨƱ��20Ԫ/�������Ϊ�˴��������Ƴ������Żݿ���
�����ۼ�600Ԫ/����ÿ��ƾ�������շ���
�������ۼ�150Ԫ/����ÿ��ƾ������10Ԫ��
�����ͨƱ���������������Żݿ��������ʹ����������������Ӿx��ʱ�������ܷ���ΪyԪ��

��1���ֱ�д��ѡ����������ͨƱ����ʱ��y��x֮��ĺ�����ϵʽ��
��2����ͬһ����ϵ�������������ѷ�ʽ��Ӧ�ĺ���ͼ����ͼ��ʾ���������A��B��C��������
��3������ݺ���ͼ����ֱ��д��ѡ���������ѷ�ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����գ��ڹ�������ͨ�����ֲ����£�ȫ�����ؽ������ڴ�����չ|һ��һ����ȫ�ػ��ж���Ϊ�˽��������綯����ͷ������ͬ�����ij����С����������˲����������ݵ������������в�������ͳ��ͼ��
��������ͳ��ͼ�ش�һ�����⣺
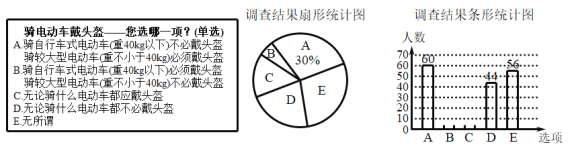
��1����ε��������_______�ˣ�
��2����ѡ��![]() ��������ѡ��
��������ѡ��![]() ��������3����������ͳ��ͼ�У�����
��������3����������ͳ��ͼ�У�����![]() ��Բ�ĽǶ�����______��
��Բ�ĽǶ�����______��
��3����ȫ����ͳ��ͼ��
��4��������Լ��80���ˣ�����ư�ȫ��ʶ������ѡ��D��E����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У�
��![]() ��
��![]() ����ǣ�
����ǣ�![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ���е㣬����
���е㣬����![]() ����
����![]() ����
����![]() �ij��� ��
�ij��� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
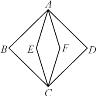
����Ŀ�����壺��ͼ��������AECF��������ABCD��������A��C�غϣ�������������E��F��������ABCD���ڲ����������AECFΪ������ABCD���ں����Σ�
�������ε��ܳ�Ϊ16�����ں����α߳������������ں����ε��ܳ�Ϊ________��
�������ε����Ϊ18�����ں����ε����Ϊ6�����ں����εı߳�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ����һֱ��������AOB��OΪ����ԭ�㣬OA=1��tan��BAO=3��������������ԭ��O��ʱ����ת90�����õ���DOC��������y=ax2+bx+c������A��B��C��
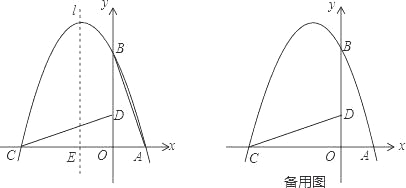
��1���������ߵĽ���ʽ��
��2������P�ǵڶ��������������ϵĶ��㣬�������Ϊt��
���������߶Գ���l��x�ύ��һ��E������PE����CD��F���������CEF����COD����ʱ����P�����ꣻ
���Ƿ����һ��P��ʹ��PCD�������������ڣ������PCD����������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ���һö���ؼ��Σ�������˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض���������ÿö�ƽ���x����ÿö������y������������ã�������
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
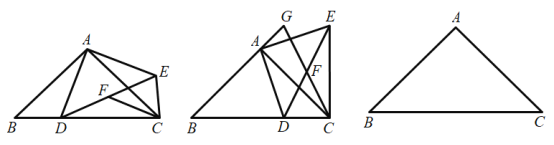
��![]() ����D��BC����һ���㣬����AD����AD�Ƶ�A��ʱ����ת90�����õ�AE������CE��DE����F��DE���е㣬����CF��
����D��BC����һ���㣬����AD����AD�Ƶ�A��ʱ����ת90�����õ�AE������CE��DE����F��DE���е㣬����CF��
��1����֤��![]() ��
��
��2����ͼ2��ʾ���ڵ�D�˶��Ĺ����У���![]() ʱ���ֱ��ӳ�CF��BA���ཻ�ڵ�G������AG��BC���ڵ�������ϵ����֤�������Ľ��ۣ�
ʱ���ֱ��ӳ�CF��BA���ཻ�ڵ�G������AG��BC���ڵ�������ϵ����֤�������Ľ��ۣ�
��3���ڵ�D�˶��Ĺ����У����߶�AD�ϴ���һ��P��ʹ![]() ��ֵ��С����
��ֵ��С����![]() ��ֵȡ����Сֵʱ��AP�ij�Ϊm����ֱ���ú�m��ʽ�ӱ�ʾCE�ij���
��ֵȡ����Сֵʱ��AP�ij�Ϊm����ֱ���ú�m��ʽ�ӱ�ʾCE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com