
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() 是锐角,
是锐角,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ;若
;若![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】作图题:(要求保留作图痕迹,不写作法)

(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);
(2)连结BE,若AC=10,AB=6,求△ABE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形地块![]() ,
,![]() 米,
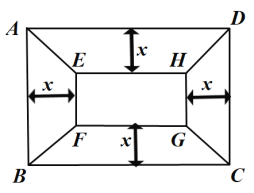
米,![]() 米,为美观,拟种植不同的花卉,如图所示,将矩形
米,为美观,拟种植不同的花卉,如图所示,将矩形![]() 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为
分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为![]() 米.现决定在等腰梯形
米.现决定在等腰梯形![]() 和
和![]() 中种植甲种花卉;在等腰梯形
中种植甲种花卉;在等腰梯形![]() 和
和![]() 中种植乙种花卉;在矩形
中种植乙种花卉;在矩形![]() 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米
中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米![]() 、60 元/米
、60 元/米![]() 、40元/米
、40元/米![]() ,设三种花卉的种植总成本为
,设三种花卉的种植总成本为![]() 元.
元.
(1)当![]() 时,求种植总成本
时,求种植总成本![]() ;
;
(2)求种植总成本![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120米![]() ,求三种花卉的最低种植总成本.
,求三种花卉的最低种植总成本.
查看答案和解析>>
科目:初中数学 来源: 题型:
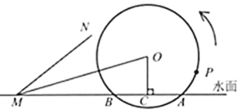
【题目】筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为![]() 的筒车
的筒车![]() 按逆时针方向每分钟转
按逆时针方向每分钟转![]() 圈,筒车与水面分别交于点
圈,筒车与水面分别交于点![]() 、
、![]() ,筒车的轴心
,筒车的轴心![]() 距离水面的高度
距离水面的高度![]() 长为
长为![]() ,简车上均匀分布着若干个盛水筒.若以某个盛水筒
,简车上均匀分布着若干个盛水筒.若以某个盛水筒![]() 刚浮出水面时开始计算时间.
刚浮出水面时开始计算时间.

(1)经过多长时间,盛水筒![]() 首次到达最高点?
首次到达最高点?
(2)浮出水面3.4秒后,盛水筒![]() 距离水面多高?
距离水面多高?
(3)若接水槽![]() 所在直线是
所在直线是![]() 的切线,且与直线
的切线,且与直线![]() 交于点
交于点![]() ,
,![]() .求盛水筒
.求盛水筒![]() 从最高点开始,至少经过多长时间恰好在直线
从最高点开始,至少经过多长时间恰好在直线![]() 上.(参考数据:
上.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
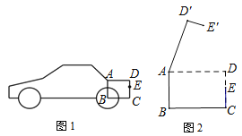
【题目】如图是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角是50度时,箱盖落在![]() 的位置(如图2),已知
的位置(如图2),已知![]()
![]()
![]()
(1)求点![]() 到
到![]() 的距离;(结果保留整数)
的距离;(结果保留整数)
(2)求![]() 两点之间的距离.(结果保留整数)
两点之间的距离.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式![]() 的几何意义是数轴上
的几何意义是数轴上![]() 所对应的点与2所对应的点之间的距离;因为
所对应的点与2所对应的点之间的距离;因为![]() ,所以
,所以![]() 的几何意义就是数轴上
的几何意义就是数轴上![]() 所对应的点与
所对应的点与![]() 所对应的点之间的距离.
所对应的点之间的距离.
⑴. 发现问题:代数式![]() 的最小值是多少?
的最小值是多少?
⑵. 探究问题:如图,点![]() 分别表示的是
分别表示的是![]() ,
,![]() .
.
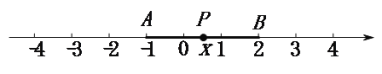
∵![]() 的几何意义是线段
的几何意义是线段![]() 与
与![]() 的长度之和
的长度之和
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点点
;当点点![]() 在点
在点![]() 的左侧或点
的左侧或点![]() 的右侧时
的右侧时 ![]()
∴![]() 的最小值是3.
的最小值是3.
⑶.解决问题:
①.![]() 的最小值是 ;
的最小值是 ;
②.利用上述思想方法解不等式:![]()
![]()
③.当![]() 为何值时,代数式
为何值时,代数式![]() 的最小值是2.
的最小值是2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料解答下列问题
观察下列方程:①![]() ,②
,②![]() ,③
,③![]() ……
……
⑴按此规律写出关于x的第n个方程为____________________,此方程的解为____________.
⑵根据上述结论,求出![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
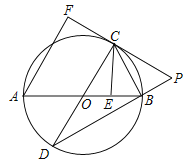
【题目】(2017广东省)如图,AB是⊙O的直径,AB=![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当![]() 时,求劣弧
时,求劣弧![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生掌握垃圾分类知识的情况,增强学生环保意识,某学校举行了“垃圾分类人人有责”的知识测试活动,现从该校七、八年级中各随机抽取20名学生的测试成绩(满分10分,6分及6分以上为合格)进行整理、描述和分析,下面给出了部分信息.
七年级20名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6.
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示:
年级 | 平均数 | 众数 | 中位数 | 8分及以上人数所占百分比 |
七年级 | 7.5 | a | 7 | 45% |
八年级 | 7.5 | 8 | b | c |
八年级20名学生的测试成绩条形统计图如图:
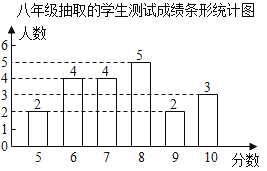
根据以上信息,解答下列问题:
(1)直接写出上述表中的a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由(写出一条理由即可);
(3)该校七、八年级共1200名学生参加了此次测试活动,估计参加此次测试活动成绩合格的学生人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com