
����Ŀ��Ͳ�����ҹ��Ŵ�����ˮ�������Ĺ�ȹ��ߣ��ƴ���͢���ڡ�ˮ�ָ�����д������ˮ������������ɡ�����ͼ���뾶Ϊ![]() ��Ͳ��
��Ͳ��![]() ����ʱ�뷽��ÿ����ת
����ʱ�뷽��ÿ����ת![]() Ȧ��Ͳ����ˮ��ֱ��ڵ�
Ȧ��Ͳ����ˮ��ֱ��ڵ�![]() ��
��![]() ��Ͳ��������
��Ͳ��������![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() ��Ϊ
��Ϊ![]() �����Ͼ��ȷֲ������ɸ�ʢˮͲ������ij��ʢˮͲ
�����Ͼ��ȷֲ������ɸ�ʢˮͲ������ij��ʢˮͲ![]() �ո���ˮ��ʱ��ʼ����ʱ�䣮
�ո���ˮ��ʱ��ʼ����ʱ�䣮

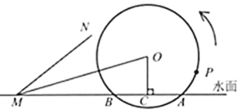
��1�������ʱ�䣬ʢˮͲ![]() �״ε�����ߵ㣿
�״ε�����ߵ㣿
��2������ˮ��3.4���ʢˮͲ![]() ����ˮ���ߣ�
����ˮ���ߣ�
��3������ˮ��![]() ����ֱ����
����ֱ����![]() �����ߣ�����ֱ��
�����ߣ�����ֱ��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����ʢˮͲ
����ʢˮͲ![]() ����ߵ㿪ʼ�����پ����ʱ��ǡ����ֱ��
����ߵ㿪ʼ�����پ����ʱ��ǡ����ֱ��![]() �ϣ����ο����ݣ�
�ϣ����ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
���𰸡���1��27.4�룻��2��0.7m����3��7.6��
��������
��1���ȸ���Ͳ��Ͳ��ÿ������ת���ٶȼ����Ͳ��ÿ����ת���ٶȣ����������Ǻ���ȷ��![]() ������ټ��������ʱ�伴�ɣ�
������ټ��������ʱ�伴�ɣ�
��2���ȸ���ʱ����ٶȼ����![]() �������ó�
�������ó�![]() ������������Ǻ��������
������������Ǻ��������![]() ���Ӷ��õ�ʢˮͲ
���Ӷ��õ�ʢˮͲ![]() ����ˮ��ĸ߶ȣ�
����ˮ��ĸ߶ȣ�
��3����ȷ����![]() ��ֱ��
��ֱ��![]() ��ʱ����ʱ
��ʱ����ʱ![]() ���е㣬���������Ǻ����õ�
���е㣬���������Ǻ����õ�![]() ��
��
![]() ���Ӷ������
���Ӷ������![]() ������ټ����ʱ�伴�ɣ�
������ټ����ʱ�伴�ɣ�
��1����ͼ1��������ã�Ͳ��ÿ����ת![]() ��
��
����![]() ����
����![]() ��
��![]() ������
������![]() ��
��
����![]() ���룩��
���룩��
��ʢˮͲ![]() �״ε�����ߵ�����ʱ��Ϊ27.4�룮
�״ε�����ߵ�����ʱ��Ϊ27.4�룮
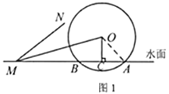
��2����ͼ2��ʢˮͲ![]() ����ˮ��3.4���ʱ
����ˮ��3.4���ʱ![]() ��
��
����![]() ��
��
����![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
�𣺴�ʱʢˮͲ![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() ��
��
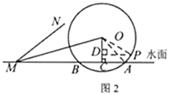
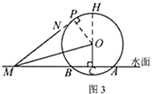
��3����ͼ3����Ϊ��![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ����
����
���Ե�![]() ��ֱ��
��ֱ��![]() ��ʱ����ʱ
��ʱ����ʱ![]() ���е㣮
���е㣮
����![]() ������
������![]() ��
��
��![]() ��
��![]() ������
������![]() ��
��
��![]() ��
��![]() ������
������![]() ��
��
����![]() ��
��
������Ҫ��ʱ��Ϊ![]() ���룩��
���룩��
�𣺴���ߵ㿪ʼ�˶���7.6���ʢˮͲ![]() ǡ����ֱ��
ǡ����ֱ��![]() �ϣ�
�ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��Ƹ�˲ţ���ӦƸ�߷ֱ�����Ķ�������˼ά�����ͱ�������������ԣ����мס������˵ijɼ����±�����λ���֣���
��Ŀ��Ա | �Ķ����� | ˼ά���� | �������� |
�� | 93 | 86 | 73 |
�� | 95 | 81 | 79 |
��1������ʵ����Ҫ����˾���Ķ���˼ά�ͱ�������������Ե÷ְ�3��5��2�ı�ȷ��ÿ�˵����ɼ�,�����˳ɼ��ڼס���������¼��һ�ˣ�˭����¼�ã�
��2����˾���գ�1���еijɼ����㷽������ÿλӦƸ�ߵ����ɼ����Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ��ÿ������ξ����������ֵ���������Ҷ���ֵ�������ұ�һ�����xΪ��85��x��90�����������ɸ߷ֵ��ͷ�¼��8��Ա�����ס��������ܷ�¼�ã���˵�����ɣ������������Ƹ�˲ŵ�¼���ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ú�ɫ���Ӱڳɵ�����ͼ�������������Ĺ��ɰ���ȥ����10��������ͼ����Ҫ��ɫ���ӵĸ���Ϊ�� ��

![]()


A.148B.152C.174D.202
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ӿ����ͨƱ��20Ԫ/�������Ϊ�˴��������Ƴ������Żݿ���
�����ۼ�600Ԫ/����ÿ��ƾ�������շ���
�������ۼ�150Ԫ/����ÿ��ƾ������10Ԫ��
�����ͨƱ���������������Żݿ��������ʹ����������������Ӿx��ʱ�������ܷ���ΪyԪ��

��1���ֱ�д��ѡ����������ͨƱ����ʱ��y��x֮��ĺ�����ϵʽ��
��2����ͬһ����ϵ�������������ѷ�ʽ��Ӧ�ĺ���ͼ����ͼ��ʾ���������A��B��C��������
��3������ݺ���ͼ����ֱ��д��ѡ���������ѷ�ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
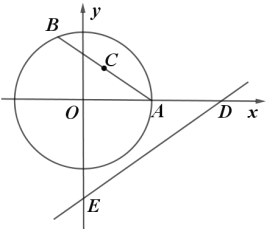
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У��뾶Ϊ2��
�У��뾶Ϊ2��![]() ��
��![]() ��������ύ�ڵ�
��������ύ�ڵ�![]() ����
����![]() ��
��![]() ��һ���㣬��
��һ���㣬��![]() Ϊ��
Ϊ��![]() ���е㣬ֱ��
���е㣬ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() �������СֵΪ________��
�������СֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����գ��ڹ�������ͨ�����ֲ����£�ȫ�����ؽ������ڴ�����չ|һ��һ����ȫ�ػ��ж���Ϊ�˽��������綯����ͷ������ͬ�����ij����С����������˲����������ݵ������������в�������ͳ��ͼ��
��������ͳ��ͼ�ش�һ�����⣺
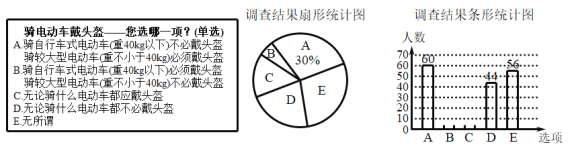
��1����ε��������_______�ˣ�
��2����ѡ��![]() ��������ѡ��
��������ѡ��![]() ��������3����������ͳ��ͼ�У�����
��������3����������ͳ��ͼ�У�����![]() ��Բ�ĽǶ�����______��
��Բ�ĽǶ�����______��
��3����ȫ����ͳ��ͼ��
��4��������Լ��80���ˣ�����ư�ȫ��ʶ������ѡ��D��E����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У�
��![]() ��
��![]() ����ǣ�
����ǣ�![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ���е㣬����
���е㣬����![]() ����
����![]() ����
����![]() �ij��� ��
�ij��� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ����һֱ��������AOB��OΪ����ԭ�㣬OA=1��tan��BAO=3��������������ԭ��O��ʱ����ת90�����õ���DOC��������y=ax2+bx+c������A��B��C��
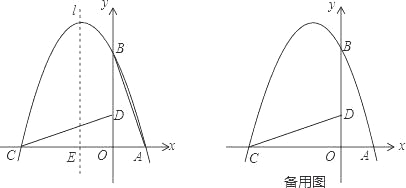
��1���������ߵĽ���ʽ��
��2������P�ǵڶ��������������ϵĶ��㣬�������Ϊt��
���������߶Գ���l��x�ύ��һ��E������PE����CD��F���������CEF����COD����ʱ����P�����ꣻ
���Ƿ����һ��P��ʹ��PCD�������������ڣ������PCD����������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����λͬѧ���о�����![]() ��
��![]() �dz�����ʱ�����ֵ�
�dz�����ʱ�����ֵ�![]() ʱ����������Сֵ���ҷ���
ʱ����������Сֵ���ҷ���![]() �Ƿ���
�Ƿ���![]() ��һ�����������ֺ�������СֵΪ3�������ֵ�
��һ�����������ֺ�������СֵΪ3�������ֵ�![]() ʱ��
ʱ��![]() ����֪����λͬѧ��ֻ��һλ���ֵĽ����Ǵ���ģ����ͬѧ�ǣ� ��
����֪����λͬѧ��ֻ��һλ���ֵĽ����Ǵ���ģ����ͬѧ�ǣ� ��
A.��B.��C.��D.��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com