
【题目】如图,已知抛物线y=ax2+bx+c(a<0,c>0)与x轴交于A,B两点,与y轴交于点C,其对称轴l为x=﹣1,直线y=kx+m经过A,C两点,与抛物线的对称轴l交于点D,且AD=2CD,连接BC,BD.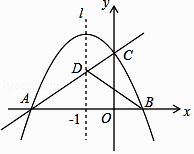
(1)求A,B两点的坐标;
(2)求证:a=﹣k;
(3)若△BCD是直角三角形,求抛物线的解析式.
【答案】
(1)
解:如图,设对称轴l与x轴的交点为E,
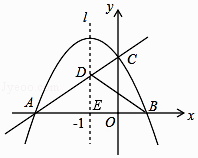
∵l∥y轴,
∴ ![]() =
= ![]() ,且AD=2DC,
,且AD=2DC,
∴AE=2EO,
∵对称轴l为x=1,
∴E(﹣1,0),则EO=1,
∴AE=2,则OA=3,
∴A(﹣3,0),
∵A、B关于对称轴l对称,
∴BE=AE=2,则OB=1,
∴B(1,0)
(2)
证明:∵抛物线经过A(﹣3,0)和B(1,0),
∴抛物线解析式为y=a(x+3)(x﹣1),即y=ax2+2ax﹣3a,
∵抛物线与y轴交于点C,
∴C(0,﹣3a),
∵直线y=kx+m经过A、C两点,
∴ ![]() ,解得m=3k,
,解得m=3k,
∴C(0,3k),
∴﹣3a=3k,即a=﹣k
(3)
解:由(1)、(2)可知B(1,0),C(0,3k),D(﹣1,2k),
∴BC2=1+9k2,BD2=4+4k2,CD2=1+k2,
∵在Rt△BCO中,∠CBD<∠CBO<90°,
∴∠CBD为锐角,
∴只可能当∠BCD或∠BDC为直角时,△BCD才是直角三角形,
①当∠BCD为直角时,则有BC2+CD2=BD2,
∴1+9k2+1+k2=4+4k2,即k2= ![]() ,
,
∵k>0,
∴k= ![]() ,
,
∴a=﹣k=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ;
;
②当∠BDC为直角时,则有BD2+CD2=BC2,
∴4+4k2+1+k2=1+9k2,即k2=1,
∵k>0,
∴k=1,
∴a=﹣k=﹣1,
∴抛物线解析式为y=﹣x2﹣2x+3;
综上可知抛物线解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() 或y=﹣x2﹣2x+3
或y=﹣x2﹣2x+3
【解析】(1)设对称轴x与x轴交点为E,由平行线分线段成比例可求得AE的长,则可求得A点坐标,再利用抛物线的对称性可求得B点坐标;(2)把A、B两点的坐标代入抛物线解析式,可用a表示出C点的坐标,再由直线AC的解析式可用k表示出C点坐标,则可得到a和k的关系;(3)用k可表示出C、D的坐标,利用勾股定理可表示出BC2、BD2和CD2 , 分∠BDC=90°和∠BCD=90°两种情况可分别求得k的值,可求得k的值,可求得a的值,则可求出抛物线的解析式.


科目:初中数学 来源: 题型:
【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[![]() ]=1.现对72进行如下操作:72
]=1.现对72进行如下操作:72![]() [
[![]() ]=8
]=8![]() [
[![]() ]=2
]=2![]() [
[![]() ]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
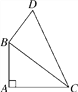
【题目】如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在一张长方形纸条上画一条数轴.
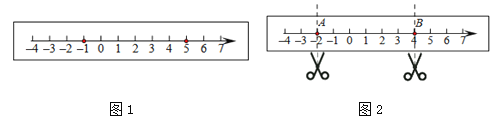
(1)折叠纸条使数轴上表示![]() 的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
(2)如果数轴上两点之间的距离为8,经过(1)的折叠方式能够重合,那么左边这个点表示的数是 ;
(3)如图2,点A、B表示的数分别是![]() 、
、![]() ,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
(4)如图2,若将此纸条沿A、B两处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折![]() 次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含
次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别做出了一次函数l1和l2的图像,l1与坐标轴的交点分别为点A、点B,l1与l2的交点为点C,但被同桌小英不小心用墨水给部分污染了,我们一起来探讨
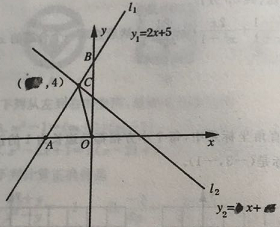
(1)写出点A、点C的坐标:A(①,0);C(②,4);
(2)求△BOC的面积:S△BOC=③
(3)直接写出不等式2x+5<·x+·的解集并回答下面问题
在解决问题(3)时,小明和小英各抒己见.小明:“l2的表达式中已经看不清楚了,并且只知道l2上一个点C的坐标,求不出该直线的表达式,所以无法求出该不等式的解集”小英说:“不用求出l2的表达式就可以得出该不等式的解集.”你同意谁的说法?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
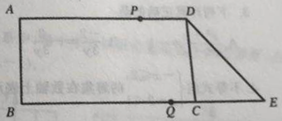
【题目】如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)求DE的长
(2)当t为多少时,四边形PQED成为平行四边形;
(3)请直接写出使得△DQE是等腰三角形时t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一次函数y=kx+b的图象,以下说法中正确的是( )

A. 直线与y轴的交点为(3,0) B. y随x的增大而增大
C. 直线与两坐标轴围成的三角形面积是6 D. 一元一次方程kx+b=0的解为x=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com