
.已知抛物线y=﹣
 x2+
x2+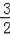
 x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )
x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )
A.
 B.
B.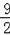
 C.
C.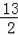
 D.
D.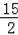

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
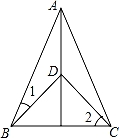
A.大40° B.小40° C.大30° D.小30°
查看答案和解析>>
科目:初中数学 来源: 题型:
作图与证明:
(1)读下列语句,作出符合题意的图形(要求:使用直尺和圆规作图,保留作图痕迹).
①作线段AB;
②分别以A,B为圆心,以AB长为半径作弧,两弧在线段AB的同侧交于点C;
③连接AC,以点C为圆心,以AB长为半径作弧,交AC延长线于点D;
④连接BD,得△ABD.
(2)求证:△ABD是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+2)2﹣3 B.y=(x+2)2+3 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
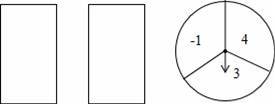
小云玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com