
将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+2)2﹣3 B.y=(x+2)2+3 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
A【考点】二次函数图象与几何变换.
【分析】先确定抛物线y=x2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)平移后所得对应点的坐标为(﹣2,﹣3),然后根据顶点式写出平移后的抛物线解析式.
【解答】解:抛物线y=x2的顶点坐标为(0,0),把点(0,0)向左平移1个单位,再向下平移2个单位长度所得对应点的坐标为(﹣2,﹣3),所以平移后的抛物线解析式为y=(x+2)2﹣3.
故选:A.
【点评】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.


科目:初中数学 来源: 题型:
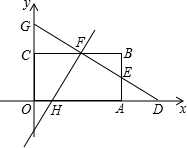
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.
(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
先阅读下面的内容,然后再解答问题.
例:已知m2+2mn+2n2﹣2n+1=0.求m和n的值.
解:∵m2+2mn+2n2﹣2n+1=0,
∴m2+2mn+n2+n2﹣2n+1=0.
∴(m+n)2+(n﹣1)2=0.
∴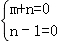 .
.
解这个方程组,得: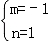 .
.
解答下面的问题:
(1)如果x2+y2﹣8x+10y+41=0成立.求(x+y)2016的值;
(2)已知a,b,c为△ABC的三边长,若a2+b2+c2=ab+bc+ca,试判断△ABC的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件是必然事件的是( )
A.有两边及一角对应相等的两三角形全等
B.若a2=b2 则有a=b
C.方程x2﹣x+1=0有两个不等实根
D.圆的切线垂直于过切点的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
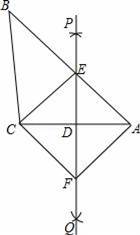
如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于
 AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com