
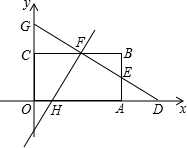
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.
(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
【考点】一次函数综合题.
【分析】(1)由顶点B的坐标为(6,4),E为AB的中点,可求得点E的坐标,又由过点D(8,0),利用待定系数法即可求得直线DE的函数关系式;
(2)由(1)可求得点F的坐标,又由函数y=mx﹣2的图象经过点F,利用待定系数法即可求得m值;
(3)首先可求得点H与G的坐标,即可求得CG,OC,CF,OH的长,然后由S四边形OHFG=S梯形OHFC+S△CFG,求得答案.
【解答】解:(1)设直线DE的解析式为:y=kx+b,
∵顶点B的坐标为(6,4),E为AB的中点,
∴点E的坐标为:(6,2),
∵D(8,0),
∴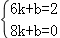 ,
,
解得: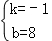 ,
,
∴直线DE的函数关系式为:y=﹣x+8;
(2)∵点F的纵坐标为4,且点F在直线DE上,
∴﹣x+8=4,
解得:x=4,
∴点F的坐标为;(4,4);
∵函数y=mx﹣2的图象经过点F,
∴4m﹣2=4,
解得:m= ;
;
(3)由(2)得:直线FH的解析式为:y= x﹣2,
x﹣2,
∵ x﹣2=0,
x﹣2=0,
解得:x=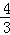 ,
,
∴点H(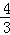 ,0),
,0),
∵G是直线DE与y轴的交点,
∴点G(0,8),
∴OH=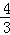 ,CF=4,OC=4,CG=OG﹣OC=4,
,CF=4,OC=4,CG=OG﹣OC=4,
∴S四边形OHFG=S梯形OHFC+S△CFG=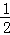 ×(
×(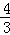 +4)×4+
+4)×4+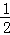 ×4×4=18
×4×4=18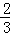 .
.
【点评】此题考查了待定系数法求一次函数的解析式、中点坐标的求解方法以及多边形的面积问题.此题难度较大,注意掌握数形结合思想与方程思想的应用.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
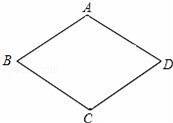
已知▱ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求▱ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
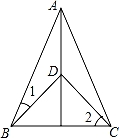
A.大40° B.小40° C.大30° D.小30°
查看答案和解析>>
科目:初中数学 来源: 题型:
齐鲁网2015年12月7日讯,中国科学院和中国工程院院士增选名单正式出炉,中国海洋大学山东微山县籍宋微波教授,当选中国科学院生命科学和医学学部院士,他主要从事海洋纤毛虫领域的研究.纤毛虫作为原生动物中特化程度最高且最为复杂的一个门,是单细胞真核生物,具有高度的形态和功能多样性,其最小个体大约有0.00002米.那么其中数据0.00002用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+2)2﹣3 B.y=(x+2)2+3 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
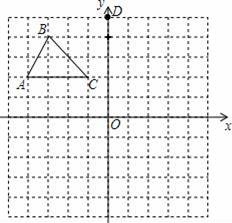
如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(﹣1,2).
(1)画出△ABC绕点D(0,5)逆时针旋转90°后的△A1B1C1;并标出A1,B1,C1的坐标.
(2)画出△ABC关于原点O的中心对称图形△A2B2C2,并标出A2,B2,C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com