
已知▱ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求▱ABCD的面积.
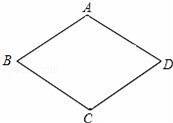

【考点】菱形的判定与性质;根的判别式;平行四边形的性质.
【分析】(1)四边形ABCD是菱形时,AB=AD,由一元二次方程根的判别式=0即可求出m的值;
(2)连接AC、BD交于点O,由一元二次方程的根求出AB的长,进一步利用菱形的性质和30°角的直角三角形的性质求得对角线的长,利用面积计算方法计算得出答案即可.
【解答】解:(1)四边形ABCD是菱形时,AB=AD,
∵AB,AD的长是关于x的方程x2﹣mx+4=0的两个实数根,
∴△=(﹣4)2﹣4m=0,
解得:m=4,
∴当m=4时,四边形ABCD是菱形
(2)如图,连接AC、BD交于点O,
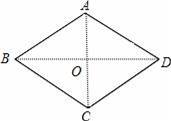

当m=4时,
x2﹣4x+4=0,
解得:x1=x2=2,
则AB=2,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABO=
 ∠ABC=30°,
∠ABC=30°,
D═2OB,AC=2OA,AC⊥BD,
在直角△AOB中,
∵∠ABO=30°,
∴OA=
 AB=1,
AB=1,
0B=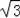
 ,
,
BD=2OB=2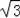
 ,
,
AC=2OA=2,
∴S菱形ABCD=
 BD•AC=
BD•AC=
 ×2×2
×2×2
 =2
=2
 .
.
【点评】本题考查了菱形的判定与性质,一元二次方程根的判别式;熟练掌握菱形性质,含30°角的直角三角形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:
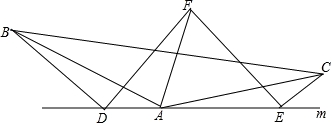
如图,在△ABC中,AB=AC,D、A、E在直线m上,∠ADB=∠AEC=∠BAC.
(1)求证:DE=DB+EC;
(2)若∠BAC=120°,AF平分∠BAC,且AF=AB,连接FD、FE,请判断△DEF的形状,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
布袋中有红、黄、蓝三种不同颜色的球各一个,从中先摸出一个球,记录下颜色后不放回布袋,将布袋搅匀,再摸出一个球,这时摸出的两个球是“一红一黄”的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2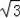
 cm,求弦AE的长.
cm,求弦AE的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
若函数y=(k﹣1)x|k|+b+1是正比例函数,则k和b的值为( )
A.k=±1,b=﹣1 B.k=±1,b=0 C.k=1,b=﹣1 D.k=﹣1,b=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
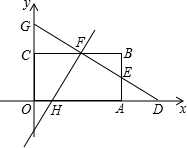
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.
(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com