
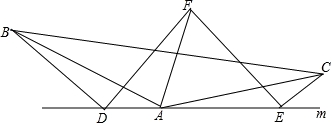
如图,在△ABC中,AB=AC,D、A、E在直线m上,∠ADB=∠AEC=∠BAC.
(1)求证:DE=DB+EC;
(2)若∠BAC=120°,AF平分∠BAC,且AF=AB,连接FD、FE,请判断△DEF的形状,并写出证明过程.
【考点】全等三角形的判定与性质.
【分析】(1)由∠ADB=∠AEC=∠BAC,于是得到∠ADB+∠ABD+∠BAD=∠BAD+∠BAC+∠EAC=180°,推出∠ABD=∠EAC,证得△ABD≌△AEC,根据全等三角形的性质得到BD=AE,然后根据线段的和差即可得到结论;
(2)由等边三角形的性质就可以求出∠BAC=120°,就可以得出△BAD≌△ACE,就有BD=AE,进而得出△BDF≌△AEF,得出DF=EF,∠BFD=∠AFE,进而得出∠DFE=60°,就有△DEF为等边三角形.
【解答】(1)证明:∵∠ADB=∠AEC=∠BAC,
∴∠ADB+∠ABD+∠BAD=∠BAD+∠BAC+∠EAC=180°,
∴∠ABD=∠EAC,
在△ABD与△ACE中,
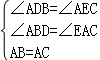 ,
,
∴△ABD≌△AEC,
∴BD=AE,
∵DE=AD+AE,
∴DE=DB+EC;
(2)△DEF为等边三角形
理由:∵△ABF和△ACF均为等边三角形
∴BF=AF=AB=AC=CF,∠BAF=∠CAF=∠ABF=60°,
∴∠BDA=∠AEC=∠BAC=120°,
∴∠DBA+∠DAB=∠CAE+∠DAB=60°,
∴∠DBA=∠CAE.
在△BAD和△ACE中,
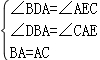 ,
,
∴△ADB≌△CEA(AAS),
∴BD=AE,∠DBA=∠CAE.
∵∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE.
在△BDF和△AEF中,
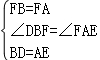 ,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
【点评】本题考查了全等三角形的判定及性质的运用.等边三角形的判定及性质的运用,等式的性质的运用,解答时证明三角形的全等是关键.


科目:初中数学 来源: 题型:
下列命题中,真命题的个数是( )
①对角线互相平分的四边形是平行四边形.②两组对角分别相等的四边形是平行四边形.③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
某区对参加市模拟考试的8000名学生的数学成绩进行抽样调查,抽取了部分学生的数学成绩(分数为整数)进行统计,并将统计结果绘制成频数分布直方图,如图所示,已知从左到右五个小组的频数之比依次是6∶7∶11∶4∶2,第五小组的频数是40.
(1) 本次调查共抽取了多少名学生?
(2) 若72分以上(含72分)为及格,96分以上(含96分)为优秀,那么抽取的学生中,及格的人数.优秀的人数各占所抽取的学生数的百分比是多少?
(3) 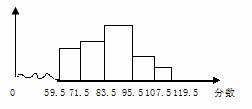 根据(2)中的结论,该区所有参加市模拟考试的学生中,及格人数.优秀人数各约为多少?
根据(2)中的结论,该区所有参加市模拟考试的学生中,及格人数.优秀人数各约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知▱ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求▱ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com