练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

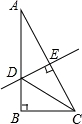
    如图，在Rt△ABC中，∠B=90°，CD平分∠ACB，过点D作DE⊥AC于点E，若AE=4，AB=10，则△ADE的周长为__________．


    14．

    【考点】角平分线的性质．

    【分析】根据角平分线的性质得到BD=DE，求得AD+DB=AD+DE=AB=10，即可得到结论．

    【解答】解：∵CD平分∠ACB，∠B=90°，DE⊥AC，

    ∴BD=DE，

    ∴AD+DB=AD+DE=AB=10，

    ∴△ADE的周长=AD+DE+AE=10+4=14．

    故答案为：14．

    【点评】本题考查的是角平分线的性质，熟知角平分线上的点到角两边的距离相等是解答此题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     描点法画函数图象的一般步骤是：①          ;②           ;③         

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某车间对生产的零件进行抽样调查，在10天中，该车间生产的零件次品数如下（单位:个）：0，3，0，1，2，1，4，2，1，3，在这10天中，该车间生产的零件次品数的

    A.中位数是2     B.平均数是1         C.众数是1          D.以上均不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是(     )

    A．（x2）3=x5 B．a+2a=3a2

    C．（﹣mn）5÷（﹣mn）3=m2n2  D．a3•a4=a12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    因式分解：a2（x﹣y）﹣4（x﹣y）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


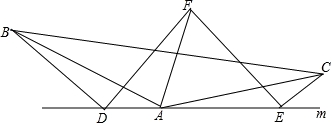
    如图，在△ABC中，AB=AC，D、A、E在直线m上，∠ADB=∠AEC=∠BAC．

    （1）求证：DE=DB+EC；

    （2）若∠BAC=120°，AF平分∠BAC，且AF=AB，连接FD、FE，请判断△DEF的形状，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


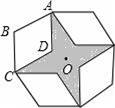
    如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=2，则图中阴影部分的面积为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=﹣x2+2x的图象可能是（　　）

    A．     B．    C．     D．

    　

    查看答案和解析>>

    同步练习册答案