
【题目】(10分)如图(1)在ΔABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
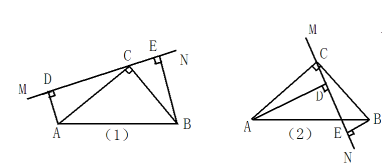
(1)求证:①ΔADC≌ΔCEB ②DE=AD+BE
(2)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE 有怎样的关系?并加以证明.
【答案】详见解析.
【解析】
试题分析:(1)由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于点E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,所以AD=CE,DC=BE,即可得到DE=DC+CE=BE+AD.(2)根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=BE,所以DE=CE-CD=AD-BE.
试题解析:(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于点E,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°∠BCE+∠CBE=90°,
∴∠ACD=∠CBE.
在△ADC和△CEB中,
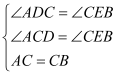
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
DE=AD-BE;理由如下:
在△ADC和△CEB中,
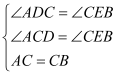
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE =CE-CD=AD-BE;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
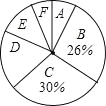
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com