练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知⊙O的半径OA=1，弦AB=1，求弦AB所对的圆周角的度数．

    分析 根据弦长等于半径，得这条弦和两条半径组成了等边三角形，则弦所对的圆心角是60°，要计算它所对的圆周角，应考虑两种情况：当圆周角的顶点在优弧上时，则根据圆周角定理，得此圆周角是30°；当圆周角的顶点在劣弧上时，则根据圆内接四边形的对角互补，得此圆周角是150°．

    解答 解：根据题意，∵弦AB与两半径组成等边三角形，
    ∴AB所对的圆心角=60°，
    ①圆周角在优弧上时，圆周角=30°，
    ②圆周角在劣弧上时，圆周角=180°-30°=150°．
    综上所述，弦AB所对圆周角的度数为30°或150°．

    点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如果代数式（2x2+ax-2y+4）-（2bx2-2x+3y-1）的值与字母x所取的值无关，试求代数式a-2b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．在-1$\frac{1}{2}$，1.2，-2，0，-（-2），（-1）3中，负数的个数有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图是一个按某种规律排列的数阵：

    根据数阵的规律，第n行第一个数是$\sqrt{{n}^{2}-n+1}$．（用含n的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

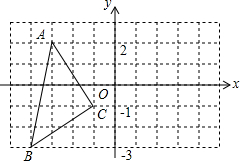    17．如图，在平面直角坐标系xOy中，
    （1）画出△ABC关于y轴的对称图形△A1B1C1；
    （2）直接写出△ABC关于x轴对称的三角形△A2B2C2的各顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．实验：袋中装有8个黑球，4个白球，这些球的形状、大小、质地等完全相同，在看不到的条件下，随机地从袋子中摸出1个球．
    我们把“摸到黑球”记为事件A，吧“摸到白球”记为事件B，填写下表并回答问题．
      事件A发生的次数事件B发生的次数  结果（指哪个事件发生的次数多）
     10次摸球   
     20次摸球   
    （1）事件A和事件B是随机事件吗？
    （2）哪个事件发生的可能性大？
    （3）你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论？
    （4）为了尽可能获得正确结论，我们应该怎样做？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．利用不等式的基本性质解不等式：
    （1）-5x+5＜-10
    （2）-$\frac{1}{2}$x+4＞-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．在平面直角坐标系中，若将抛物线y=-（x+3）2+1先向左平移2个单位长度，再向下平移3个单位长度，则经过这两次平移后所得抛物线的顶点坐标是（-5，-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

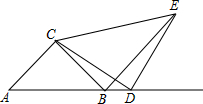    18．如图，已知△ABC，CA=CB，DC=DE，∠BCA=∠CDE=90°，D是AB延长线上一点．
    （1）求证：CB⊥EB；
    （2）求证：2AD-AB=$\sqrt{2}$EB；
    （3）若CE=2，AC=$\sqrt{2}$，点F与点D关于CE对称，连BF，则S△EBF=1．

    查看答案和解析>>

    同步练习册答案