
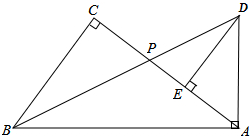
 如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.分析 (1)要证∠CBP=∠ABP,只需证∠BPC=∠BDA即可,而题目告诉AP=AD,结论显然;
(2)①设AB的长为x,则BC可用x表示,用勾股定理建立方程即可解出x;要求△ABP的面积,只需求出AB边上的高即可,由(1)知BP是角平分线,所以作PF垂直AB于点F,可得BF=BC,PF=PC,从而AF=4,设PF=y,则AP=8-y,再用勾股定理解出y即可;
②证△PFA≌△AED即可得出AE=PF.
解答 解:(1)∵∠C=90°,
∴∠CBP+∠BPC=90°,
∵DA⊥BA,
∴∠PBA+∠BDA=90°,
∵AD=AP,
∴∠BDA=∠DPA=∠BPC,
∠CBP=∠ABP;
(2)①设AB=x,
∵AB-BC=4,
∴BC=x-4,
∵AC=8,
∴在Rt△ABC中,(x-4)2+64=x2,
解得:x=10,
即AB=10,
∴BC=6,
过点P作PF⊥BA于点F,如图,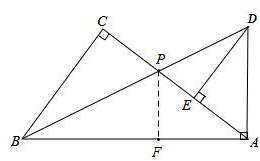
在△BCP和△BFP中:
$\left\{\begin{array}{l}{∠CBP=∠FBP}\\{∠BCP=∠BFP}\\{BP=BP}\end{array}\right.$,
∴△BCP≌△BFP(AAS),
∴BF=BC=6,PF=PC,
∴AF=4,
设PF=PC=y,
在Rt△PAF中,16+y2=(8-y)2,
解得:y═3,
即PF=3,
∴${S}_{△ABP}=\frac{1}{2}×AB×PF$=$\frac{1}{2}×10×3$=15;
③∵DE⊥AC,
∴∠EAD+∠ADE=90°=∠PAF+∠EAD,
∠PAF=∠ADE,
在△PAF和△ADE中,
$\left\{\begin{array}{l}{∠PFA=∠AED}\\{∠PAF=∠ADE}\\{PA=AD}\end{array}\right.$,
∴△PAF≌△ADE(AAS),
∴AE=PF=3.
点评 本题主要考查了等腰三角形的性质、角平分线的性质、勾股定理、全等三角形的判定与性质等知识点,有一定综合性,难度适中.通过角平分线上的点向两边作垂线,从而构造全等三角形,是常用手段,务必掌握.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com