
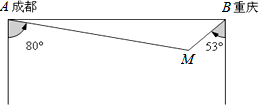
分析 (1)过M作MD⊥AB于D,直角△AMD与直角△MBD有公共边MD,根据三角函数即可利用MD表示出AD与BD,根据AB=AD+BD即可列出关于MD的方程,从而求得MD的长,与40km比较大小即可判断;
(2)在直角△MBD中,根据三角函数定义得出BM=$\frac{DM}{cos∠BMD}$,代入数值计算即可.
解答 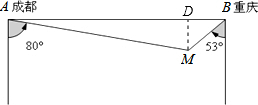 解:(1)过M作MD⊥AB于D,设DM=xkm.
解:(1)过M作MD⊥AB于D,设DM=xkm.
在直角△AMD中,tan∠AMD=$\frac{AD}{DM}$,
则AD=DM•tan∠AMD=x•tan80°≈5.67x,
同理:BD=DM•tan53°≈1.33x,
∵AB=AD+BD,
∴308=5.67x+1.33x,
∴x=44>40,
故成渝高铁不会穿越保护区;
(2)∵在直角△MBD中,∠BDM=90°,∠BMD=53°,DM=44km,
∴BM=$\frac{DM}{cos∠BMD}$≈$\frac{44}{0.60}$≈73.3(km).
即重庆到森林保护区中心BM的距离约为73.3km.
点评 本题主要考查了解直角三角形的应用-方向角问题,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:选择题
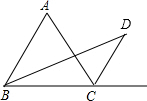 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )
如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )| A. | 15° | B. | 25° | C. | 30° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
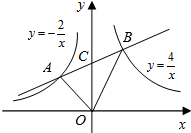 如图,点A是反比例函数y=-$\frac{2}{x}$在第二象限内图象上一点,点B是反比例函数y=$\frac{4}{x}$在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
如图,点A是反比例函数y=-$\frac{2}{x}$在第二象限内图象上一点,点B是反比例函数y=$\frac{4}{x}$在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
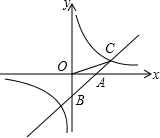 如图,一次函数y=x+b的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{2}{x}$交于点C(2,m),则点B到OC的距离是( )
如图,一次函数y=x+b的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{2}{x}$交于点C(2,m),则点B到OC的距离是( )| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{2}{5}\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得${S_{△O{P_{2014}}{P_{2015}}}}$=$\frac{\sqrt{2015}}{2}$.
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得${S_{△O{P_{2014}}{P_{2015}}}}$=$\frac{\sqrt{2015}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com