
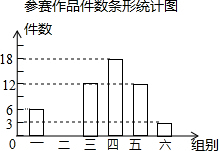
 某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:
某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:
| 10 |
| 18 |
| 5 |
| 9 |
| 2 |
| 3 |
| 6 |
| 9 |
| 5 |
| 9 |
| 6 |
| 9 |


科目:初中数学 来源: 题型:
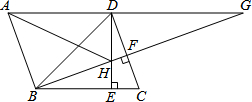 如图,?ABCD中,∠DBC=45°,高线DE、BF交于点H,BF、AD的延长线交于点G;联结AH.
如图,?ABCD中,∠DBC=45°,高线DE、BF交于点H,BF、AD的延长线交于点G;联结AH.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
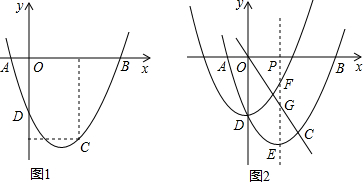
 如图,一次函数y=kx+b的图象交x轴于点A(4,0),与y轴正半轴交于点B,cos∠BAO=
如图,一次函数y=kx+b的图象交x轴于点A(4,0),与y轴正半轴交于点B,cos∠BAO=| 4 |
| 5 |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
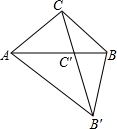 如图,在三角形ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠ABC的度数是
如图,在三角形ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠ABC的度数是查看答案和解析>>
科目:初中数学 来源: 题型:
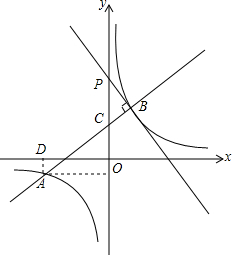 已知:直线y=
已知:直线y=| 3 |
| 4 |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com