
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| 3 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| 3 |
| 2 |
| 25 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| 3 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
| 销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
查看答案和解析>>
科目:初中数学 来源: 题型:
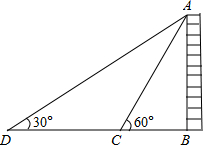 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?
如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
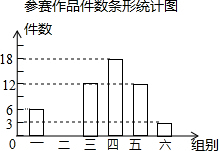 某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:
某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com