
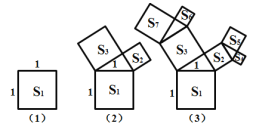
【题目】请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为____________(其中图 中出现的三角形均是直角三角形,四边形均是正方形).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
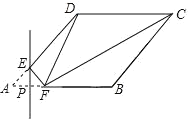
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为![]() 的三角形面积。
的三角形面积。
问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为![]() 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB=![]() 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=![]() 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC=![]() 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
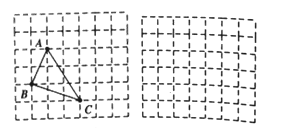
(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为![]() 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
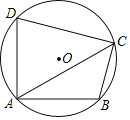
【题目】已知四边形ABCD内接于⊙O,∠DAB=90°.
(Ⅰ)若AB=AD,求∠ACB的度数;
(Ⅱ)连接AC,若AD=8,AB=6,对角线AC平分∠DAB,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com