
分析 先将原式化简,然后将a=$\sqrt{2}$代入化简后的式子,即可求得相应的值,注意本题的原式要有意义,则分母不等于0,除式不等于0,从而可以发现a不等于1、-1、0.
解答 解:($\frac{1}{a}$-$\frac{2}{a-1}$)÷$\frac{a^2+a}{1-2a+a^2}$
=$\frac{a-1-2a}{a(a-1)}×\frac{(a-1)^{2}}{a(a+1)}$
=$\frac{-(a+1)}{a(a-1)}×\frac{(a-1)^{2}}{a(a+1)}$
=$\frac{1-a}{{a}^{2}}$,
当a=$\sqrt{2}$时,原式=$\frac{1-\sqrt{2}}{(\sqrt{2})^{2}}$=$\frac{1-\sqrt{2}}{2}$.
点评 本题考查分式的化简求值,解题的关键是明确题意,选取合适的a的值,注意挖掘题目中的隐含条件,原式中的分母和除式都不等于0.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{AM}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
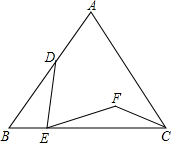 如图,在等边△ABC中,D、E分别为AB、BC边上的动点,满足AD=2BE,将线段DE绕点E顺时针旋转60°得线段EF,求证:CF平分∠ACB.
如图,在等边△ABC中,D、E分别为AB、BC边上的动点,满足AD=2BE,将线段DE绕点E顺时针旋转60°得线段EF,求证:CF平分∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com