
分析 将第2、3两个方程相减消去x,与第1个方程构成二元一次方程组,解关于y、z的二元一次方程组求得y、z的值,再代回方程求出x的值即可.
解答 解:解方程组$\left\{\begin{array}{l}{y+z=3}&{①}\\{x+2y+z=8}&{②}\\{x+y+2z=7}&{③}\end{array}\right.$,
②-③,得:y-z=1 ④,
①-④,得:z=1,
将z=1代入①,得:y=2,
将y=2,z=1代入②,得:x+4+1=8,
解得;x=3,
所以方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=1}\end{array}\right.$.
点评 本题主要考查了三元一次方程组的解法,①首先利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组.②然后解这个二元一次方程组,求出这两个未知数的值.③再把求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个关于第三个未知数的一元一次方程.④解这个一元一次方程,求出第三个未知数的值.⑤最后将求得的三个未知数的值用“{,”合写在一起即可.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
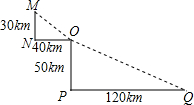 如图是某沿江地区交通平面图,其中,MN⊥ON,OP⊥QP.为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是100万元/km,该沿江高速公路的造价预计是多少?
如图是某沿江地区交通平面图,其中,MN⊥ON,OP⊥QP.为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是100万元/km,该沿江高速公路的造价预计是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com