
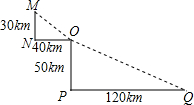
 如图是某沿江地区交通平面图,其中,MN⊥ON,OP⊥QP.为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是100万元/km,该沿江高速公路的造价预计是多少?
如图是某沿江地区交通平面图,其中,MN⊥ON,OP⊥QP.为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是100万元/km,该沿江高速公路的造价预计是多少? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
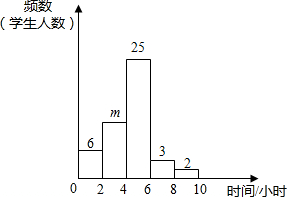 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
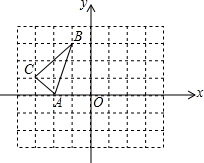 如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com