
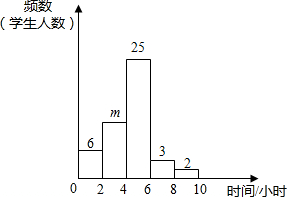
 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:分析 (1)由直方图与随机抽查了50名初三学生,即可求得答案;
(2)首先求得算50名学生的课外活动时间的平均数,继而可对初三年级全体学生平均每周的课外活动吋问做个推断;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与其中至少有1人课外活动时间在8~10小时的情况,再利用概率公式即可求得答案.
解答 解:(1)m=50-6-25-3-2=14;
(2)∵$\overline{x}$=$\frac{1×6+3×14+5×25+7×3+9×2}{50}$=4.24,
∴估计初三年级全体学生平均每周的课外活动时间为:4.24小时;
(3)分别用A,B表示在6~8小时与在8~10小时的学生,
画树状图得: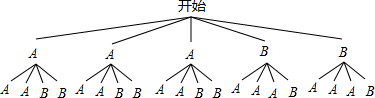
∵共有20种等可能的结果,其中至少有1人课外活动时间在8~10小时的有14种情况,
∴其中至少有1人课外活动时间在8~10小时的概率为:$\frac{14}{20}$=$\frac{7}{10}$.
点评 此题考查了列表法或树状图法求概率以及直方图的知识.用到的知识点为:概率=所求情况数与总情况数之比.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
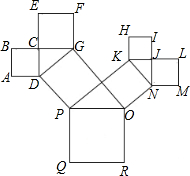 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形ABCD,正方形CEFG,正方形KHIJ,正方形JLMN的边长分别是3,5,2,3,则最大正方形ROPQ的面积是( )
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形ABCD,正方形CEFG,正方形KHIJ,正方形JLMN的边长分别是3,5,2,3,则最大正方形ROPQ的面积是( )| A. | 13 | B. | 26 | C. | 47 | D. | 94 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
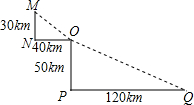 如图是某沿江地区交通平面图,其中,MN⊥ON,OP⊥QP.为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是100万元/km,该沿江高速公路的造价预计是多少?
如图是某沿江地区交通平面图,其中,MN⊥ON,OP⊥QP.为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是100万元/km,该沿江高速公路的造价预计是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
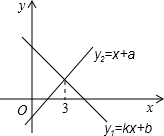 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③不等式kx+b<x+a的解集为x<3中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③不等式kx+b<x+a的解集为x<3中,正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
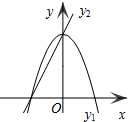 已知抛物线y1=-2x2+2和直线y2=2x+2的图象如图所示,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.则下列结论中一定成立的是②④(把所有正确结论的序号都填在横线上)
已知抛物线y1=-2x2+2和直线y2=2x+2的图象如图所示,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.则下列结论中一定成立的是②④(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com