
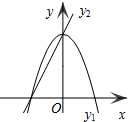
 已知抛物线y1=-2x2+2和直线y2=2x+2的图象如图所示,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.则下列结论中一定成立的是②④(把所有正确结论的序号都填在横线上)
已知抛物线y1=-2x2+2和直线y2=2x+2的图象如图所示,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.则下列结论中一定成立的是②④(把所有正确结论的序号都填在横线上)分析 若y1=y2,记M=y1=y2.首先求得抛物线与直线的交点坐标,利用图象可得当x>0时,利用函数图象可以得出y2>y1;当-1<x<0时,y1>y2;当x<-1时,利用函数图象可以得出y2>y1;然后根据当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;即可求得答案.
解答 解:∵当y1=y2时,即-2x2+2=2x+2时,
解得:x=0或x=-1,
∴当x>0时,利用函数图象可以得出y2>y1;当-1<x<0时,y1>y2;当x<-1时,利用函数图象可以得出0>y2>y1;
∴①不成立;
∵抛物线y1=-2x2+2的最大值为2,故M大于2的x值不存在,
∴②成立;
∵抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;
∴③不成立;
∵如图:当-1<x<0时,y1>y2;
当M=1,2x+2=1,x=-$\frac{1}{2}$;
x>0时,y2>y1;
当M=1,-2x2+2=1,x1=$\frac{\sqrt{2}}{2}$,x2=-$\frac{\sqrt{2}}{2}$(舍去),
∴使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$,
∴④成立;
故答案为:②④.
点评 本题主要考查了二次函数与一次函数综合应用.注意掌握函数增减性是解题关键,注意数形结合思想与方程思想的应用.


科目:初中数学 来源: 题型:解答题
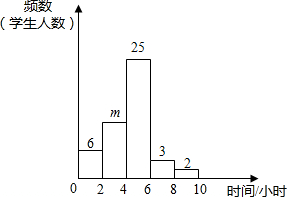 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
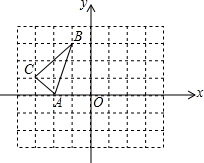 如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com