
分析 (1)直接利用韦达定理,把a,b看作是一元二次方程x2-2x-1=0两个根求出答案;
(2)接利用韦达定理,把m,n2看作是一元二次方程x2-2x+a=0两个根求出答案;
(3)利用已知得出ab,a+b,看作是一元二次方程x2-9x+20=0两个根,进而得出答案.
解答 解:(1)对于a2-2a-1=0,b2-2b-1=0两个方程.
我们可以把a,b看作是一元二次方程x2-2x-1=0两个根,
由韦达定理可得:a+b=2;
故答案为:2;
(2)对于m2-2m+a=0,n4-2n2+a=0,两个方程.
我们可以把m,n2看作是一元二次方程x2-2x+a=0两个根,
由韦达定理可得:$\frac{1}{{n}^{2}}$+$\frac{1}{m}$=$\frac{{n}^{2}+m}{{n}^{2}m}$=$\frac{2}{a}$=-2,
解得:a=-1;
故答案为:-1;
(3)∵ab+a+b=9,a2b+ab2=ab(a+b)=20,
∴设ab,a+b,看作是一元二次方程x2-9x+20=0两个根,由a,b是正整数,
解得:a+b=5,ab=4,
∴a2+b2=(a+b)2-2ab=25-8=17.
点评 此题主要考查了根与系数的关系,正确应用韦达定理是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
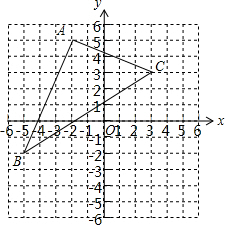 如图,已知△ABC各顶点的坐标分别为A(-2,5)B(-5,-2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.
如图,已知△ABC各顶点的坐标分别为A(-2,5)B(-5,-2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com