【题目】如图，△ABC中，AB = AC，AD、AE分别是∠BAC和∠BAC外角的平分线，
．
（1）求证：DA⊥AE；
（2）试判断AB与DE是否相等？并证明你的结论．
【答案】（1）证明见解析；（2）AB=DE．证明见解析．
【解析】
试题(1)、根据角平分线的性质可得∠BAD=
∠BAC，∠BAE=∠BAF，根据平角的性质可以得出结论；(2)、根据等于三角形的三线合一定理说明∠ADB=90°，根据三个角是直角的四边形为矩形得出ADBE为矩形，最后根据矩形的对角线的性质说明结论.
试题解析：(1)、∵AD、AE分别为角平分线 ∴∠BAD=∠BAC，∠BAE=∠BAF
∵∠BAC+∠BAF=180° ∴∠BAD+∠BAE=(∠BAC+∠BAF)=90° ∴DA⊥AE
、∵AB=AC AD为角平分线 ∴AD⊥BC 即∠ADB=90°
∵BE⊥AE ∴∠BEA=90° 又∵∠DAE=90° ∴四边形ADBE为矩形 ∴AB=DE
春雨教育同步作文系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△DEB中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是
A．BC=EC，∠B=∠E B．BC=EC，AC=DC
C．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇，下表是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
（进价、售价均保持不变，利润=销售收入-进货成本）
（1）求A、B两种型号的电风扇的销售单价；
（2）若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
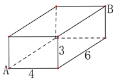
【题目】如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）
A. 
cm B. 
cm C. 
cm D. 9cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对非负实数x“四舍五入”到个位的值记为<x>，即当n为非负整数时，若
，则<x>＝n，如<0.46>=0，<3.67>=4。给出下列关于<x>的结论：
①<1.493>=1；
②<2x>=2<x>；
③若
，则实数x的取值范围是
；
④当x≥0，m为非负整数时，有
；
⑤
。
其中，正确的结论有 （填写所有正确的序号）。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列各式，属于二元一次方程的个数有（ ）
①xy+2x﹣y＝7；②4x+1＝x﹣y；③
+y＝5；④x＝y；⑤x2﹣y2＝2；⑥6x﹣2y；⑦x+y+z＝1；⑧y（y﹣1）＝2x2﹣y2+xy
A.1B.2C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在□ABCD中，点E是边CD的中点，连接BE并延长，交AD延长线于点F，连接BD、CF.
（1）求证：△CEB≌△DEF；
（2）若AB=BF，试判断四边形BCFD的形状，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
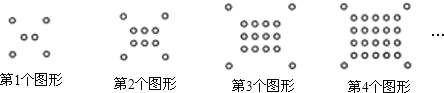
【题目】将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，…，依次规律，第9个图形圆的个数为（ ）
A.94B.85C.84D.76
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（数学经验）三角形的中线的性质：三角形的中线等分三角形的面积．
（经验发展）面积比和线段比的联系：
（1）如图1，M为△ABC的AB上一点，且BM=2AM．若△ABC的面积为a，若△CBM的面积为S，则S=_______(用含a的代数式表示)．
（结论应用）（2）如图2，已知△CDE的面积为1，
，
，求△ABC的面积．
（迁移应用）（3）如图3．在△ABC中，M是AB的三等分点(
)，N是BC的中点，若△ABC的面积是1，请直接写出四边形BMDN的面积为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com