
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点A,正方形ABCD的顶点B在
轴交于点A,正方形ABCD的顶点B在![]() 轴上,点D在直线
轴上,点D在直线![]() 上,且AO=OB,反比例函数
上,且AO=OB,反比例函数![]() (
(![]() )经过点C.
)经过点C.
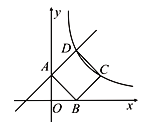
(1)求一次函数和反比例函数的解析式;
(2)点P是![]() 轴上一动点,当
轴上一动点,当![]() 的周长最小时,求出P点的坐标;
的周长最小时,求出P点的坐标;
(3)在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.
【答案】(1)y=x+2,![]() ;(2)P(
;(2)P(![]() ,0);(3)M的坐标为(
,0);(3)M的坐标为(![]() ,2),(
,2),(![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).
【解析】
(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,利用一次函数图象上点的坐标特征、正方形的性质以及等腰三角形的性质可得出点E的坐标,由点E的坐标利用待定系数法可求出一次函数解析式,由BD∥OA,OE=OB可求出BD的长,进而可得出点D的坐标,由正方形的性质可求出点C的坐标,再利用反比例函数图象上点的坐标特征可求出反比例函数解析式;
(2)作点D关于x轴的对称点D',连接CD'交x轴于点P,此时△PCD的周长取最小值,由点D的坐标可得出点D'的坐标,由点C,D'的坐标,利用待定系数法可求出直线CD'的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(3)设点M的坐标为(x,y),分DP为对角线、CD为对角线及CP为对角线三种情况,利用平行四边形的性质(对角线互相平分)可求出点M的坐标,此题得解.
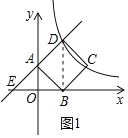
(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,如图1所示.
当x=0时,y=kx+2=2,∴OA=2.
∵四边形ABCD为正方形,OA=OB,∴∠BAE=90°,∠OAB=∠OBA=45°,∴∠OAE=∠OEA=45°,∴OE=OA=2,点E的坐标为(﹣2,0).
将E(﹣2,0)代入y=kx+2,得:﹣2k+2=0,解得:k=1,∴一次函数的解析式为y=x+2.
∵∠OBD=∠ABD+∠OBA=90°,∴BD∥OA.
∵OE=OB=2,∴BD=2OA=4,∴点D的坐标为(2,4).
∵四边形ABCD为正方形,∴点C的坐标为(2+2﹣0,0+4﹣2),即(4,2).
∵反比例函数y![]() (x>0)经过点C,∴n=4×2=8,∴反比例函数解析式为y
(x>0)经过点C,∴n=4×2=8,∴反比例函数解析式为y![]() .
.
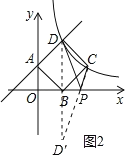
(2)作点D关于x轴的对称点D',连接CD'交x轴于点P,此时△PCD的周长取最小值,如图2所示.
∵点D的坐标为(2,4),∴点D'的坐标为(2,﹣4).
设直线CD'的解析式为y=ax+b(a≠0),将C(4,2),D'(2,﹣4)代入y=ax+b,得:![]() ,解得:
,解得:![]() ,∴直线CD'的解析式为y=3x﹣10.
,∴直线CD'的解析式为y=3x﹣10.
当y=0时,3x﹣10=0,解得:x![]() ,∴当△PCD的周长最小时,P点的坐标为(
,∴当△PCD的周长最小时,P点的坐标为(![]() ,0).
,0).
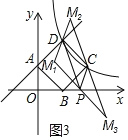
(3)设点M的坐标为(x,y),分三种情况考虑,如图3所示.
①当DP为对角线时,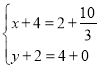 ,解得:
,解得:![]() ,∴点M1的坐标为(
,∴点M1的坐标为(![]() ,2);
,2);
②当CD为对角线时,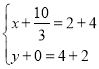 ,解得:
,解得:![]() ,∴点M2的坐标为(
,∴点M2的坐标为(![]() ,6);
,6);
③当CP为对角线时,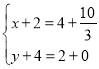 ,解得:
,解得: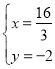 ,∴点M3的坐标为(
,∴点M3的坐标为(![]() ,﹣2).
,﹣2).
综上所述:以点C、D、P为顶点作平行四边形,第四个顶点M的坐标为(![]() ,2),(
,2),(![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
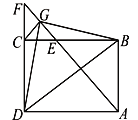
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG、BG、BD、DG,下列结论:① BC=DF,②∠DGF=135o;③BG⊥DG,④ 若3AD=4AB,则4S△BDG=25S△DGF;正确的是____________(只填番号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级师生为了响应“绿水青山就是金山银山”的号召,在今年3月的植树月活动中到某荒山植树,如图是抽查了其中20名师生植树棵数的统计图.
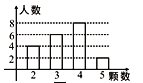
(1)求这20名师生种树棵数的平均数、众数、中位数;
(2)如果该校八年级共有师生500名,所植树的存活率是90%,估计所植的树共有多少棵存活?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD垂直平分AC,垂足为F,分别过点B作直线BE∥AD,过点A作直线EA⊥AC于点A,两直线交于点E.

(1)求证:四边形AEBD是平行四边形;
(2)如果∠ABE=∠ABD=60°,AD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A. b2﹣c2=a2B. a:b:c=3:4:5
C. ∠A:∠B:∠C=9:12:15D. ∠C=∠A﹣∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥![]() 于点D.
于点D.
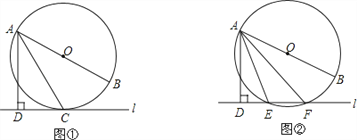
(1)如图①,当直线![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
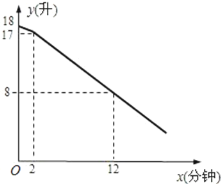
【题目】教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,它们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;
(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?
(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com