
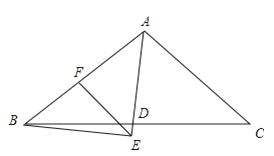
【题目】如图,在△ABC中,AD平分∠BAC,BE⊥AD,BE交AD的延长线于点E,点F在AB上,且EF∥AC.求证:点F是AB的中点.
【答案】详见解析.
【解析】
由AD为角平分线可得再由∠BAE=∠CAE,由EF∥AC,根据两直线平行内错角相等可得∠AEF=∠CAE,所以∠AEF=∠BAE,根据等角对等边即可得AF=EF.又因∠BAE+∠ABE=90°,∠BEF+∠AEF=90°,∠AEF=∠BAE,利用等角的余角相等可得出∠BEF=∠ABE,根据等角对等边得到即可得BF=EF,所以AF=BF,即F为AB的中点.
证明:∵AD平分∠BAC,
∴∠BAE=∠CAE,
∵EF∥AC,
∴∠AEF=∠CAE,
∴∠AEF=∠BAE,
∴AF=EF,
又∵BE⊥AD,
∴∠BAE+∠ABE=90°,∠BEF+∠AEF=90°,
又∠AEF=∠BAE,
∴∠ABE=∠BEF,
∴BF=EF,
∴AF=BF,
∴F为AB中点.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
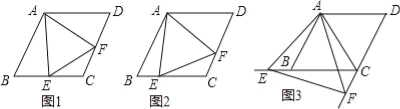
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六![]() 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
![]() 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?
![]() 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点A,正方形ABCD的顶点B在
轴交于点A,正方形ABCD的顶点B在![]() 轴上,点D在直线
轴上,点D在直线![]() 上,且AO=OB,反比例函数
上,且AO=OB,反比例函数![]() (
(![]() )经过点C.
)经过点C.
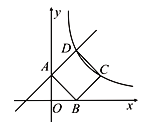
(1)求一次函数和反比例函数的解析式;
(2)点P是![]() 轴上一动点,当
轴上一动点,当![]() 的周长最小时,求出P点的坐标;
的周长最小时,求出P点的坐标;
(3)在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
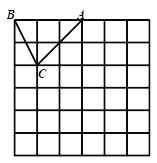
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
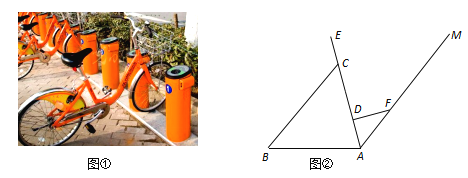
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
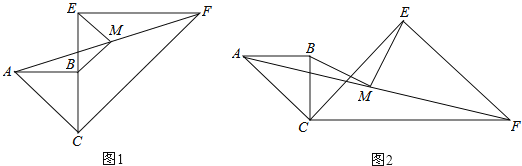
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
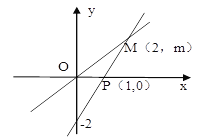
【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com