
分析 (1)根据二次根式的乘除法则运算;
(2)先把各二次根式化简为最简二次根式,然后合并即可.
解答 解:(1)原式=2×$\frac{1}{5}$×$\frac{1}{4}$×$\sqrt{12×\frac{1}{2}×3}$
=$\frac{3\sqrt{2}}{10}$;
(2)原式=6$\sqrt{2}$-3$\sqrt{2}$+$\frac{\sqrt{2}}{2}$
=$\frac{7\sqrt{2}}{2}$;
(3)原式=9+6$\sqrt{2}$+2-(4-3)
=11+6$\sqrt{2}$-1
=10+6$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD中,AD∥BC,EF分别是AB、CD的中点,线段EF交AC、BD于M、N两点,MN=1,AD<BC,且AD、BC的长是抛物线y=x2-2kx+k2-k+2与x轴两个交点的横坐标.
如图,梯形ABCD中,AD∥BC,EF分别是AB、CD的中点,线段EF交AC、BD于M、N两点,MN=1,AD<BC,且AD、BC的长是抛物线y=x2-2kx+k2-k+2与x轴两个交点的横坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
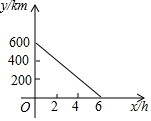 甲、乙两列车分别从A,B两站同时相对开出,甲车每小时行驶60km,如图反映的是从出发到相遇,两车之间的距离y(km)与行驶的时间x(h)之间的函数关系.根据图象回答:
甲、乙两列车分别从A,B两站同时相对开出,甲车每小时行驶60km,如图反映的是从出发到相遇,两车之间的距离y(km)与行驶的时间x(h)之间的函数关系.根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
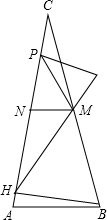 如图,△ABC中,M,N分别是BC,AC的中点,BH是AC边上的高线,∠HMN=45°,MP垂直∠HMN的平分线并交AC于点P,若PH=$\frac{1}{2}$(AB+BC),求证:△ABC是等腰三角形.
如图,△ABC中,M,N分别是BC,AC的中点,BH是AC边上的高线,∠HMN=45°,MP垂直∠HMN的平分线并交AC于点P,若PH=$\frac{1}{2}$(AB+BC),求证:△ABC是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com