
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=a![]() +bx+c(a<0)������A��B��
+bx+c(a<0)������A��B��
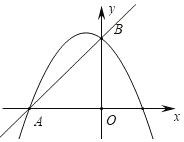
(1)��a��b����Ĺ�ϵʽ��c��ֵ��
(2)��x<0ʱ����y=a![]() +bx+c(a<0)�ĺ���ֵ��x�������������a��ȡֵ��Χ��
+bx+c(a<0)�ĺ���ֵ��x�������������a��ȡֵ��Χ��
(3)��ͼ����a=1ʱ�������������Ƿ���ڵ�P��ʹ��PAB�����Ϊ![]() ?�����ڣ�������������������е�P�����ꣻ�������ڣ���˵�����ɣ�
?�����ڣ�������������������е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��b=3a+1��c=3����2��![]() ����3����P������Ϊ����
����3����P����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��.
��.
��������
��1�������A��B�����꣬������⣻
��2����x��0ʱ����y=ax2+bx+c��a��0���ĺ���ֵ��x����������������Գ���![]() ����b=3a+1������
����b=3a+1������![]() ��������⣻
��������⣻
��3������P��ֱ��l��AB����PQ��y�ύBA�ڵ�Q����PH��AB�ڵ�H����S��PAB=![]() ����
����![]() =1��������⣮
=1��������⣮
�⣺��1��y=x+3����x=0����y=3����y=0����x=![]() ��
��
�ʵ�A��B������ֱ�Ϊ��-3��0������0��3������c=3��
��������ʽΪ��y=ax2+bx+3��
����A���������ʽ�������ã�b=3a+1��
��2����x��0ʱ����y=ax2+bx+c��a��0���ĺ���ֵ��x�����������
�����Գ���![]() ��
��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��a��ȡֵ��ΧΪ��![]() ��
��
��3����a=![]() ʱ��b=3a+1=
ʱ��b=3a+1=![]()
���κ�������ʽΪ��![]() ��
��
����P��ֱ��l��AB����PQ��y�ύBA�ڵ�Q����PH��AB�ڵ�H��
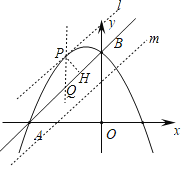
��OA=OB��
���BAO=��PQH=45�㣬
S��PAB=![]() ��AB��PH=
��AB��PH=![]() ��
��![]() ��PQ��
��PQ��![]() =
=![]() ��
��
��PQ=![]() =1��
=1��
��ֱ��AB�·���ֱ��m��ʹֱ��m��l��ֱ��AB�Ⱦ��룬
��ֱ��m���������������㣬�ֱ����AB��ɵ������ε����ҲΪ![]() ��
��
��![]() ��
��
���P��x��-x2-2x+3�������Q��x��x+3����
����-x2-2x+3-x-3=��1��
��ã�![]() ��
��![]() ��
��
���P����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾ����ƽ��ֱ������ϵ�У����κ���![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ������һ��
������һ��![]() ������
������![]() .
.
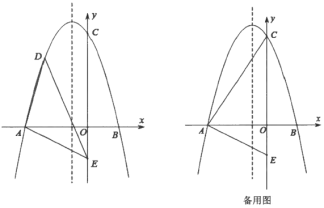
��1������κ����ı���ʽ��
��2����![]() �ǵڶ������ڵĵ���������һ����
�ǵڶ������ڵĵ���������һ����
����![]() ������ֵ��д����ʱ��
������ֵ��д����ʱ��![]() �����ꣻ
�����ꣻ
����![]() �����ʱ��
�����ʱ��![]() ���ꣻ
���ꣻ
��3������![]() ����
����![]() ���߶�
���߶�![]() �ϵĶ���.����
�ϵĶ���.����![]() �����߶�
�����߶�![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() ����
����![]() �ǵ�
�ǵ�![]() �Ķ�Ӧ��.������
�Ķ�Ӧ��.������![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ����
����![]() ��������·��������______��ֱ��д���𰸣�
��������·��������______��ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
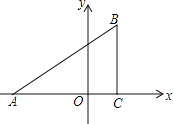
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB��90�㣬��A��C������ֱ�ΪA����3��0����C��1��0����tan��BAC��![]() ��
��
��1��д����B�����ꣻ
��2����x������һ��D������BD��ʹ�á�ADB���ABC���ƣ�������ȫ�ȣ��������D�����ꣻ
��3���ڣ�2���������£������P�ӵ�A��������2cm/����ٶ���AB���B�˶���ͬʱ��Q�ӵ�D��������1cm/����ٶ���DA���A�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�����Ƿ����������tʹ�á�APQ���ADB���ƣ�����ڣ������t��ֵ���粻���ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���![]() ��
��![]() ����ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����y��Ľ���B�ڣ�0��2���ͣ�0��3��֮�䣨���������㣩�����н��ۣ�
����ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����y��Ľ���B�ڣ�0��2���ͣ�0��3��֮�䣨���������㣩�����н��ۣ�
����x��3ʱ��y��0��
��3a+b��0��
��![]() ��
��
��![]() ��
��
������ȷ�Ľ����ǣ� ��
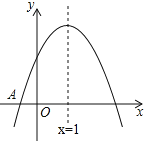
A.�٢ۢ�B.�٢ڢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���![]() ��ͼ����x���·��IJ�����x�ᷭ�۵�x���Ϸ���ͼ������ಿ�ֱ��ֲ��䣬���ۺ��ͼ����ԭͼ��x���Ϸ��IJ������һ�����硰W������ͼ����ֱ��y=-2x+b�����ͼ�����������㣬��ʵ��b��ȡֵ��Χ��__________
��ͼ����x���·��IJ�����x�ᷭ�۵�x���Ϸ���ͼ������ಿ�ֱ��ֲ��䣬���ۺ��ͼ����ԭͼ��x���Ϸ��IJ������һ�����硰W������ͼ����ֱ��y=-2x+b�����ͼ�����������㣬��ʵ��b��ȡֵ��Χ��__________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD����E��DC���ϵ�һ���㣬����C��AE�Ĵ��߽�AE�ӳ����ڵ�F����D��DH��CF������ΪH����O��AC�е㣬��HO��
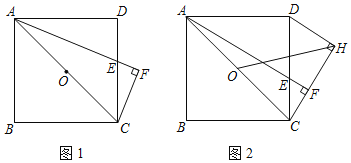
��1����ͼ1������CAE����DAEʱ��֤����AE��2CF��
��2����ͼ2������E��DC���˶�ʱ���߶�AF���߶�HO֮���Ƿ����ȷ����������ϵ�������ڣ�֤���㷢�ֵĽ��ۣ��������ڣ���˵�����ɣ�
��3����EΪDC�е�ʱ��AC��2![]() ��ֱ��д��AF�ij��� ��
��ֱ��д��AF�ij��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ���P��Բ��һ���㣬�����C�ֱ�λ��ֱ��AB�����࣬![]() ������C��
������C��![]() ��PB���ӳ����ڵ�Q��
��PB���ӳ����ڵ�Q��
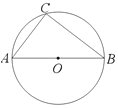
(1)����P�˶���ʲôλ��ʱ��CQǡ���ǡ�O�����ߣ�
(2)����P���C����ֱ��AB�Գƣ���AB=5�����ʱCQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
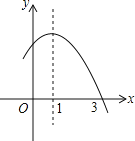
����Ŀ����֪���κ���y����x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η��̩�x2+2x+m��0�Ľ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�������![]() �Ķ���
�Ķ���![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ����һ���㣨����˵�
����һ���㣨����˵�![]() �غϣ�������
�غϣ�������![]() �����߶�
�����߶�![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
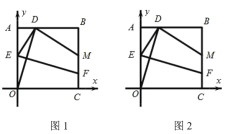
��1����ͼ1������![]() Ϊ�߶�AB���е�ʱ�����߶�
Ϊ�߶�AB���е�ʱ�����߶�![]() �ij���
�ij���
��2����ͼ2����������![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ��
��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() ����֤��
����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
��3���ڣ�2���������£��������C��������![]() ͬʱ������������������
ͬʱ������������������
��![]() ���ڵ�
���ڵ�![]() ʱ������
ʱ������![]() �����ֵΪ
�����ֵΪ![]() ���������ϵ��
���������ϵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com