
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() БпЩЯвЛЖЏЕуЃЈВЛгыЖЫЕу
БпЩЯвЛЖЏЕуЃЈВЛгыЖЫЕу![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌзїЯпЖЮ
ЃЌзїЯпЖЮ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() НЛБп
НЛБп![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
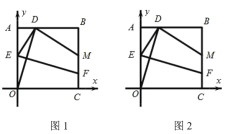
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() ЮЊЯпЖЮABЕФжаЕуЪБЃЌЧѓЯпЖЮ
ЮЊЯпЖЮABЕФжаЕуЪБЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєе§ЗНаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌ
ЃЌ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌМЧ
ЃЌМЧ![]() ЃЌЪджЄУї
ЃЌЪджЄУї![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙЙдьЙ§ЕуCЕФХзЮяЯп![]() ЭЌЪБТњзувдЯТСНИіЬѕМўЃК
ЭЌЪБТњзувдЯТСНИіЬѕМўЃК
Ђй![]() ЃЛЂкЕБ
ЃЛЂкЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌЧѓЖўДЮЯюЯЕЪ§
ЃЌЧѓЖўДЮЯюЯЕЪ§![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЖўДЮЯюЯЕЪ§
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЖўДЮЯюЯЕЪ§![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩш![]() ЃЌИљОнЙДЙЩЖЈРэСаЗНГЬПЩЕУ
ЃЌИљОнЙДЙЩЖЈРэСаЗНГЬПЩЕУ![]() ЕФжЕЃЌДгЖјЕУDEЃЌAEЕФжЕЃЌжЄУїЁїAEDЁзЁїBDMЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУDMЕФГЄЃЛ ЃЈ2ЃЉе§ЗНаЮOABCЕФжмГЄЮЊ
ЕФжЕЃЌДгЖјЕУDEЃЌAEЕФжЕЃЌжЄУїЁїAEDЁзЁїBDMЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУDMЕФГЄЃЛ ЃЈ2ЃЉе§ЗНаЮOABCЕФжмГЄЮЊ![]() ЃЌЩш
ЃЌЩш![]() ЃЌБэЪО
ЃЌБэЪО![]() ЃЌИљОнЙДЙЩЖЈРэНЈСЂ
ЃЌИљОнЙДЙЩЖЈРэНЈСЂ![]() жЎМфЕФЙиЯЕЪНЃЌгЩЃЈ1ЃЉжаЕФЯрЫЦСаБШР§ЪНПЩБэЪОBM ЃЌDM ЃЌМЦЫуЁїBMDЕФжмГЄЮЊ
жЎМфЕФЙиЯЕЪНЃЌгЩЃЈ1ЃЉжаЕФЯрЫЦСаБШР§ЪНПЩБэЪОBM ЃЌDM ЃЌМЦЫуЁїBMDЕФжмГЄЮЊ![]() ЃЌДњШыПЩЧѓЕУmЕФжЕЃЛ ЃЈ3ЃЉЯШРћгУ
ЃЌДњШыПЩЧѓЕУmЕФжЕЃЛ ЃЈ3ЃЉЯШРћгУ![]() гывбжЊЬѕМўЕУЕН
гывбжЊЬѕМўЕУЕН![]() гы
гы![]() ЕФЙиЯЕЃЌаДГіХзЮяЯпЕФНтЮіЪНЃЌПЩЕУЖдГЦжсЃЌНЋЃЈ2ЃЉжаЕФmДњШыЃКЕУЕН3ЁмxЁм7ЪБЃЌyгазюДѓжЕЃЌАДПЊПкЗНЯђЗжЧщПіЬжТлПЩЕУНсТлЃЎ
ЕФЙиЯЕЃЌаДГіХзЮяЯпЕФНтЮіЪНЃЌПЩЕУЖдГЦжсЃЌНЋЃЈ2ЃЉжаЕФmДњШыЃКЕУЕН3ЁмxЁм7ЪБЃЌyгазюДѓжЕЃЌАДПЊПкЗНЯђЗжЧщПіЬжТлПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЩш![]() ЃЌвРЬтвтгаЃК
ЃЌвРЬтвтгаЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁпEDЁЭDMЃЌ ЁрЁЯEDM=ЁЯADE+ЁЯBDM=90ЁуЃЌ
ЁпЁЯADE+ЁЯAED=90ЁуЃЌ ЁрЁЯAED=ЁЯEDMЃЌ
ЁпЁЯDAE=ЁЯMBD=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМДЯпЖЮ
ЃЌМДЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЎ
ЃЎ
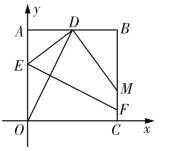
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌдђга
ЃЌдђга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌећРэЕУЃК
ЃЌећРэЕУЃК![]() ЃЎ
ЃЎ
гЩ![]() ПЩЕУЃК
ПЩЕУЃК![]() ЃЌ
ЃЌ
ДгЖјгаЃК![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌНЋ
ЃЌНЋ![]() ДњШыЃЌПЩЕУ
ДњШыЃЌПЩЕУ![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЛЁр
ЃЛЁр![]() ЮЊЖЈжЕЃЎ
ЮЊЖЈжЕЃЎ
ЃЈ3ЃЉЁпХзЮяЯп![]() ОЙ§
ОЙ§![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌЦфЖдГЦжсЮЊ
ЃЌЦфЖдГЦжсЮЊ![]() ЃЎ
ЃЎ
гЩ![]() ПЩжЊЕБ
ПЩжЊЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
гкЪЧгаЃКЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБга
ЪБга![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБга
ЪБга![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЖўДЮЯюЯЕЪ§![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
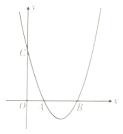
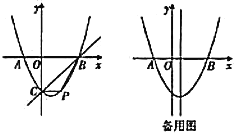
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌХзЮяЯпy=a![]() +bx+c(a<0)ОЙ§ЕуAЃЌBЃЌ
+bx+c(a<0)ОЙ§ЕуAЃЌBЃЌ
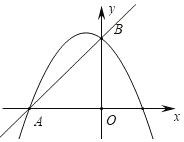
(1)ЧѓaЁЂbТњзуЕФЙиЯЕЪНМАcЕФжЕЃЌ
(2)ЕБx<0ЪБЃЌШєy=a![]() +bx+c(a<0)ЕФКЏЪ§жЕЫцxЕФдіДѓЖјдіДѓЃЌЧѓaЕФШЁжЕЗЖЮЇЃЌ
+bx+c(a<0)ЕФКЏЪ§жЕЫцxЕФдіДѓЖјдіДѓЃЌЧѓaЕФШЁжЕЗЖЮЇЃЌ
(3)ШчЭМЃЌЕБa=1ЪБЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPABЕФУцЛ§ЮЊ![]() ?ШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЫљгаЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЌ
?ШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЫљгаЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉ![]() ЃЈx+1ЃЉЃЈxЉ9ЃЉгызјБъжсНЛгкAЁЂBЁЂCШ§ЕуЃЌDЮЊЖЅЕуЃЌСЌНсACЃЌBCЃЎЕуPЪЧИУХзЮяЯпдкЕквЛЯѓЯоФкЩЯЕФвЛЕуЃЎЙ§ЕуPзїyжсЕФЦНааЯпНЛBCгкЕуEЃЌСЌНсAPНЛBCгкЕуFЃЌдђ
ЃЈx+1ЃЉЃЈxЉ9ЃЉгызјБъжсНЛгкAЁЂBЁЂCШ§ЕуЃЌDЮЊЖЅЕуЃЌСЌНсACЃЌBCЃЎЕуPЪЧИУХзЮяЯпдкЕквЛЯѓЯоФкЩЯЕФвЛЕуЃЎЙ§ЕуPзїyжсЕФЦНааЯпНЛBCгкЕуEЃЌСЌНсAPНЛBCгкЕуFЃЌдђ![]() ЕФзюДѓжЕЮЊ_______ЃЎ
ЕФзюДѓжЕЮЊ_______ЃЎ
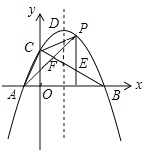
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() гы
гы![]() жсе§АыжсНЛгк
жсе§АыжсНЛгк![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌгы
зѓВрЃЉЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉРћгУжБГпКЭдВЙцЃЌзїГіХзЮяЯп![]() ЕФЖдГЦжсЃЈГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЛ
ЕФЖдГЦжсЃЈГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЛ
ЃЈ2ЃЉШє![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌЧвЦфбќГЄЮЊ3ЃЌЧѓ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌЧвЦфбќГЄЮЊ3ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕу![]() ЮЊХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌдђ
ЮЊХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌдђ![]() ЕФзюаЁжЕЮЊ________ЃЎ
ЕФзюаЁжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГХЉЛЇМЦЛЎгУГЄ12mЕФРщАЪЮЇГЩвЛИіЁАШеЁБзжаЮЕФЩњЮядАЫЧбјСНжжВЛЭЌЕФМвЧнЃЌЩњЮядАЕФвЛУцППЧНЃЌЧвЧНЕФПЩРћгУГЄЖШзюГЄЮЊ7mЃЎ
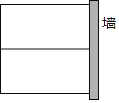
ЃЈ1ЃЉШєЩњЮядАЕФУцЛ§ЮЊ9m2ЃЌдђетИіЩњЮядАДЙжБгкЧНЕФвЛБпГЄЮЊЖрЩйЃП
ЃЈ2ЃЉШєвЊЪЙЩњЮядАЕФУцЛ§зюДѓЃЌИУдѕбљЮЇЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЗсИЛЭЌбЇУЧЕФПЮгрЩњЛюЃЌФГбЇаЃОйааЁАЧзНќДѓздШЛЁБЛЇЭтЛюЖЏЃЌЯжЫцЛњГщШЁСЫВПЗжбЇЩњНјаажїЬтЮЊЁАФузюЯыШЅЕФОАЕуЪЧЃПЁБЕФЮЪОэЕїВщЃЌвЊЧѓбЇЩњжЛФмДгЁА![]() ЃЈжВЮядАЃЉЁЂ
ЃЈжВЮядАЃЉЁЂ![]() ЃЈЖЏЮядАЃЉЁЂ
ЃЈЖЏЮядАЃЉЁЂ![]() ЃЈЪЊЕиЙЋдАЃЉЁЂ
ЃЈЪЊЕиЙЋдАЃЉЁЂ![]() ЃЈдРТДЩНЃЉЁБЫФИіОАЕужабЁдёвЛИіЃЌИљОнЕїВщНсЙћЃЌЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
ЃЈдРТДЩНЃЉЁБЫФИіОАЕужабЁдёвЛИіЃЌИљОнЕїВщНсЙћЃЌЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
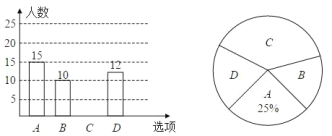
ЃЈ1ЃЉетДЮЮЪОэЕїВщЕФШЫЪ§ЪЧ_________ШЫЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉМЦЫуЁА![]() ЁБЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊ_________ЃЛ
ЁБЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊ_________ЃЛ
ЃЈ4ЃЉШєИУбЇаЃЙВга3000УћбЇЩњЃЌдђЙРМЦИУаЃзюЯыШЅдРТДЩНЕФбЇЩњдМЮЊ_________ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЗЂЯжЃК
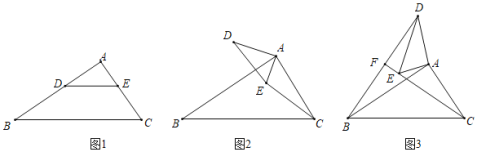
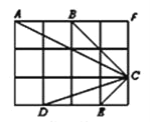
(1)ШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯAЃН90ЁуЃЌABЃНkAC(kЃО1)ЃЌDЪЧABЩЯвЛЕуЃЌDEЁЮBCЃЌдђBDЃЌECЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁЃЎ
РрБШЬНОП
(2)ШчЭМ2ЃЌНЋЁїAEDШЦзХЕуAЫГЪБеыа§зЊЃЌа§зЊНЧЮЊa(0ЁуЃМaЃМ90Ёу)ЃЌСЌНгCEЃЌBDЃЌЧыЮЪ(1)жаBDЃЌECЕФЪ§СПЙиЯЕЛЙГЩСЂТ№ЃПЫЕУїРэгЩ
ЭиеЙбгЩьЃК
(3)ШчЭМ3ЃЌдк(2)ЕФЬѕМўЯТЃЌНЋЁїAEDШЦЕуAМЬаја§зЊЃЌа§зЊНЧЮЊa(aЃО90Ёу)ЃЎжБЯпBDЃЌCEНЛгкFЕуЃЌШєACЃН1ЃЌABЃН![]() ЃЌдђЕБЁЯACEЃН15ЁуЪБЃЌBFCFЕФжЕЮЊ_____ЃЎ
ЃЌдђЕБЁЯACEЃН15ЁуЪБЃЌBFCFЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЖЅЕузјБъЮЊ
ЕФЖЅЕузјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЯТЗНХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЯТЗНХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉ![]() ЕФУцЛ§ЪЧЗёгазюДѓжЕЃПШчЙћгаЃЌЧыЧѓГізюДѓжЕКЭДЫЪБЕу
ЕФУцЛ§ЪЧЗёгазюДѓжЕЃПШчЙћгаЃЌЧыЧѓГізюДѓжЕКЭДЫЪБЕу![]() ЕФзјБъЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉ![]() ЮЊ
ЮЊ![]() жсгвВрХзЮяЯпЩЯвЛЕуЃЌ
жсгвВрХзЮяЯпЩЯвЛЕуЃЌ![]() ЮЊЖдГЦжсЩЯвЛЕуЃЌШє
ЮЊЖдГЦжсЩЯвЛЕуЃЌШє![]() ЪЧвдЕу
ЪЧвдЕу![]() ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу
ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() ЕФе§ЗНаЮЗНИёжаЃЌ
ЕФе§ЗНаЮЗНИёжаЃЌ![]() КЭ
КЭ![]() ЕФЖЅЕуЖМдкБпГЄЮЊ1ЕФаЁе§ЗНаЮЕФЖЅЕуЩЯЃЎ
ЕФЖЅЕуЖМдкБпГЄЮЊ1ЕФаЁе§ЗНаЮЕФЖЅЕуЩЯЃЎ
ЃЈ1ЃЉЬюПеЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉХаЖЯ![]() гы
гы![]() ЪЧЗёЯрЫЦЃЌВЂжЄУїФуЕФНсТлЃЎ
ЪЧЗёЯрЫЦЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com