
【题目】如图,某农户计划用长12m的篱笆围成一个“日”字形的生物园饲养两种不同的家禽,生物园的一面靠墙,且墙的可利用长度最长为7m.
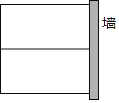
(1)若生物园的面积为9m2,则这个生物园垂直于墙的一边长为多少?
(2)若要使生物园的面积最大,该怎样围?
【答案】(1)3m;(2)生物园垂直于墙的一边长为2m.平行于墙的一边长为6m时,围成生物园的面积最大,且为12m2
【解析】
(1)设垂直于墙的一边长为x米,则平行于墙的一边长为(12-3x)米,根据长方形的面积公式结合生物园的面积为9平方米,列出方程,解方程即可;
(2)设围成生物园的面积为y,由题意可得:y=x(12﹣3x)且![]() ≤
≤![]() <4,从而求出y的最大值即可.
<4,从而求出y的最大值即可.
设这个生物园垂直于墙的一边长为xm,
(1)由题意,得x(12﹣3x)=9,
解得,x1=1(不符合题意,舍去),x2=3,
答:这个生物园垂直于墙的一边长为3m;
(2)设围成生物园的面积为ym2.
由题意,得![]() ,
,
∵![]()
∴![]() ≤
≤![]() <4
<4
∴当x=2时,y最大值=12,12﹣3x=6,
答:生物园垂直于墙的一边长为2m.平行于墙的一边长为6m时,围成生物园的面积最大,且为12m2.


科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图像在x轴下方的部分沿x轴翻折到x轴上方,图像的其余部分保持不变,翻折后的图像与原图像x轴上方的部分组成一个形如“W”的新图像,若直线y=-2x+b与该新图像有两个交点,则实数b的取值范围是__________
的图像在x轴下方的部分沿x轴翻折到x轴上方,图像的其余部分保持不变,翻折后的图像与原图像x轴上方的部分组成一个形如“W”的新图像,若直线y=-2x+b与该新图像有两个交点,则实数b的取值范围是__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,形状相同的抛物线
,形状相同的抛物线![]() 的顶点在直线
的顶点在直线![]() 上,其对称轴与
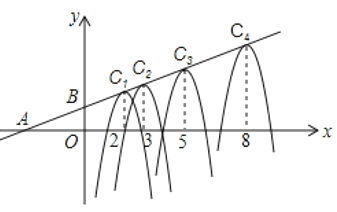
上,其对称轴与![]() 轴的交点的横坐标依次为2,3,5,18,13,…,根据上述规律,抛物线
轴的交点的横坐标依次为2,3,5,18,13,…,根据上述规律,抛物线![]() 的顶点坐标为_________.
的顶点坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,正方形![]() 的顶点
的顶点![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点(不与端点
边上一动点(不与端点![]() 重合),连接
重合),连接![]() ,作线段
,作线段![]() 的垂直平分线
的垂直平分线![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
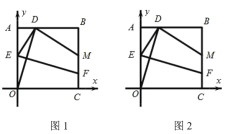
(1)如图1,当点![]() 为线段AB的中点时,求线段
为线段AB的中点时,求线段![]() 的长;
的长;
(2)如图2,若正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,记
,记![]() ,试证明
,试证明![]() 为定值;
为定值;
(3)在(2)的条件下,构造过点C的抛物线![]() 同时满足以下两个条件:
同时满足以下两个条件:
①![]() ;②当
;②当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求二次项系数
,求二次项系数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
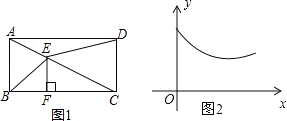
A.线段BEB.线段EFC.线段CED.线段DE
查看答案和解析>>
科目:初中数学 来源: 题型:
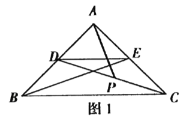
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)观察猜想
图1中,线段![]() 与
与![]() 的数量关系是______,位置关系是________;
的数量关系是______,位置关系是________;
(2)探究证明
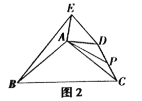
把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,小航猜想(1)中的结论仍然成立,请你证明小航的猜想;
逆时针方向旋转到图2的位置,小航猜想(1)中的结论仍然成立,请你证明小航的猜想;
(3)拓展延伸
把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件正确的是( )
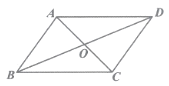
A. AB=AD B. AC=BD C. ∠ABC=90° D. ∠ABC=∠ADC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com