
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是________米(结果保留根号).

【答案】200(![]() +1)
+1)
【解析】
先根据从热气球C处测得地面A、B两点的俯角分别为30°、45°可求出∠BCD与∠ACD的度数,再由直角三角形的性质求出AD与BD的长,根据AB=AD+BD即可得出结论.
∵从热气球C处测得地面A、B两点的俯角分别为30°、45°,
∴∠BCD=90°﹣45°=45°,∠ACD=90°﹣30°=60°,
∵CD⊥AB,CD=200米,
∴△BCD是等腰直角三角形,
∴BD=CD=200米,
在Rt△ACD中,
∵CD=200米,∠ACD=60°,
∴AD=CDtan60°=200×![]() =200
=200![]() (米),
(米),
∴AB=AD+BD=200![]() +200=200(
+200=200(![]() +1)米.
+1)米.
故答案为:200(![]() +1)
+1)


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】阅读:多项式![]() 当
当![]() 取某些实数时,
取某些实数时,![]() 是完全平方式.
是完全平方式.
例如:![]() 时,
时,![]() , 发现:
, 发现: ![]() ;
;
![]() 时,
时,![]() ,发现:
,发现:![]() ;
;
![]() 时,
时,![]() , 发现:
, 发现:![]() ;
;
……
根据阅读解答以下问题:
![]() 分解因式:
分解因式: ![]()
![]() 若多项式
若多项式![]() 是完全平方式,则
是完全平方式,则![]() 之间存在某种关系,用等式表示
之间存在某种关系,用等式表示![]() 之间的关系:
之间的关系:
![]() 在实数范围内,若关于
在实数范围内,若关于![]() 的多项式
的多项式![]() 是完全平方式,求
是完全平方式,求![]() 值.
值.
![]() 求多项式:
求多项式:![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上小明用一副三角板进行如下操作:把一副三角板中两个直角的顶点重合,一个三角板固定不动,另一个三角板绕着重合的顶点旋转(两个三角板始终有重合部分).
(1)当旋转到如图所示的位置时,量出∠α=25°,通过计算得出∠AOD=∠BOC= ;
(2)通过几次操作小明发现,∠α≠25°时.∠AOD=∠BOC仍然成立,请你帮他完成下面的说理过程.
理由:因为∠AOC=∠BOD= ;
所以,根据等式的基本性质∠ ﹣∠COD=∠BOD﹣∠ ;
即∠AOD=∠ .
(3)小莹还发现在旋转过程中∠AOB和∠DOC之间存在一个不变的数量关系,请你用等式表示这个数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数![]() 上一个动点,
上一个动点,![]() 轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会
轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会![]()
![]()

A. 先增后减 B. 先减后增 C. 逐渐减小 D. 逐渐增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
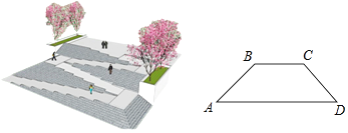
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥BD,请先作图再解决问题.
(1)利用尺规完成以下作图,并保留作图痕迹.(不要求写作法)
①作BE平分∠ABD交AC于点E;
②在BA的延长线上截取AF=BA,连接EF;
(2)判断△BEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com