
【题目】已知抛物线![]() .
.
(1)当![]() ,
,![]() 时,求抛物线
时,求抛物线![]() 与
与![]() 轴的交点个数;
轴的交点个数;
(2)当![]() 时,判断抛物线
时,判断抛物线![]() 的顶点能否落在第四象限,并说明理由;
的顶点能否落在第四象限,并说明理由;
(3)当![]() 时,过点
时,过点![]() 的抛物线
的抛物线![]() 中,将其中两条抛物线的顶点分别记为
中,将其中两条抛物线的顶点分别记为![]() ,
,![]() ,若点
,若点![]() ,
,![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,且点
,且点![]() 在第三象限.以线段
在第三象限.以线段![]() 为直径作圆,设该圆的面积为
为直径作圆,设该圆的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)抛物线![]() 与
与![]() 轴有两个交点;(2)抛物线
轴有两个交点;(2)抛物线![]() 的顶点不会落在第四象限,理由详见解析;(3)
的顶点不会落在第四象限,理由详见解析;(3)![]() .
.
【解析】
(1)将![]() ,
,![]() 代入解析式,然后求当y=0时,一元二次方程根的情况,从而求解;(2)首先利用配方法求出顶点坐标,解法一:假设顶点在第四象限,根据第四象限点的坐标特点列不等式组求解;解法二:设
代入解析式,然后求当y=0时,一元二次方程根的情况,从而求解;(2)首先利用配方法求出顶点坐标,解法一:假设顶点在第四象限,根据第四象限点的坐标特点列不等式组求解;解法二:设![]() ,
,![]() ,则
,则![]() ,分析一次函数图像所经过的象限,从而求解;(3)将点
,分析一次函数图像所经过的象限,从而求解;(3)将点![]() 代入抛物线,求得a的值,然后求得抛物线解析式及顶点坐标,分别表示出A,B两点坐标,并根据点A位于第三象限求得t的取值范围,利用勾股定理求得
代入抛物线,求得a的值,然后求得抛物线解析式及顶点坐标,分别表示出A,B两点坐标,并根据点A位于第三象限求得t的取值范围,利用勾股定理求得![]() 的函数解析式,从而求解.
的函数解析式,从而求解.
解:(1)依题意,将![]() ,
,![]() 代入解析式
代入解析式
得抛物线![]() 的解析式为
的解析式为![]() .
.
令![]() ,得
,得![]() ,
,![]() ,
,
∴抛物线![]() 与
与![]() 轴有两个交点.
轴有两个交点.
(2)抛物线![]() 的顶点不会落在第四象限.
的顶点不会落在第四象限.
依题意,得抛物线![]() 的解析式为
的解析式为![]() ,
,
∴顶点坐标为![]() .
.
解法一:不妨假设顶点坐标在第四象限,
则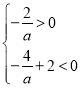 ,解得
,解得![]() .
.
∴该不等式组无解,
∴假设不成立,即此时抛物线![]() 的顶点不会落在第四象限.
的顶点不会落在第四象限.
解法二:设![]() ,
,![]() ,则
,则![]() ,
,
∴该抛物线![]() 的顶点在直线
的顶点在直线![]() 上运动,而该直线不经过第四象限,
上运动,而该直线不经过第四象限,
∴抛物线![]() 的顶点不会落在第四象限.
的顶点不会落在第四象限.
(3)将点![]() 代入抛物线
代入抛物线![]() :
:![]() ,
,
得![]() ,
,
化简,得![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴此时,抛物线![]() 的解析式为
的解析式为![]() ,
,
![]()
∴顶点坐标为![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() .
.
∵点![]() 在第三象限,∴
在第三象限,∴![]()
∴![]() .
.
又![]() ,
,![]() ,
,
∴点![]() 在点
在点![]() 的右上方,
的右上方,
∴![]() .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() .
.
又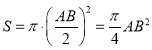 .
.
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】把函数C1:y=ax2﹣2ax﹣3a(a≠0)的图象绕点P(m,0)旋转180°,得到新函数C2的图象,我们称C2是C1关于点P的相关函数.C2的图象的对称轴与x轴交点坐标为(t,0).
(1)填空:t的值为 (用含m的代数式表示)
(2)若a=﹣1,当![]() ≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
(3)当m=0时,C2的图象与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段AD原点O逆时针旋转90°,得到它的对应线段A′D′,若线A′D′与C2的图象有公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生某科目学期总评成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果学期总评成绩80分以上(含80分),则评定为“优秀”,下表是小张和小王两位同学的成绩记录:
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 | _______ |
若按完成作业、单元检测、期末考试三项成绩按1:2:7的权重来确定学期总评成绩.
(1)请计算小张的学期总评成绩为多少分?
(2)小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣3)2+![]() (a≠0)过点C(0,4),顶点为M,与x轴交于A,B两点.如图所示以AB为直径作圆,记作⊙D.
(a≠0)过点C(0,4),顶点为M,与x轴交于A,B两点.如图所示以AB为直径作圆,记作⊙D.
(1)试判断点C与⊙D的位置关系;
(2)直线CM与⊙D相切吗?请说明理由;
(3)在抛物线上是否存在一点E,能使四边形ADEC为平行四边形.
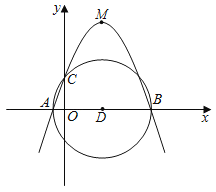
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+2x+6交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分別交x轴、线段AC于点E、F.
x2+2x+6交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分別交x轴、线段AC于点E、F.
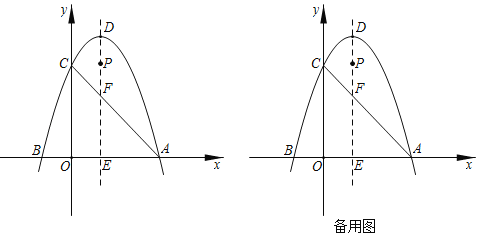
(1)求抛物线的对称轴及点A的坐标;
(2)连结AD,CD,求△ACD的面积;
(3)设动点P从点D出发,沿线段DE匀速向终点E运动,取△ACD一边的两端点和点P,若以这三点为顶点的三角形是等腰三角形,且P为顶角顶点,求所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
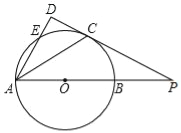
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=![]() ,AD=6,求线段AE的长.
,AD=6,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机下载一个APP,缴纳一定数额的押金,就能以每小时0.5到1元的价格解锁一辆自行车任意骑行…最近的网红非“共享单车”莫属.共享单车为解决市民出行的“最后一公里”难题帮了大忙,人们在享受科技进步、共享经济带来的便利的同时,随意停放、加装私锁、大卸八块等毁坏单车的行为也层出不穷.某共享单车公司一月投入部分自行车进入市场,一月底发现损坏率不低于10%,二月初又投入1200辆进入市场,使可使用的自行车达到7500辆.
(1)一月份该公司投入市场的自行车至少有多少辆?
(2)二月份的损坏率达到20%,进入三月份,该公司新投入市场的自行车比二月份增长4a%,由于媒体的关注,毁坏共享单车的行为引起了一场国民素质的大讨论,三月份的损坏率下降![]() a%,三月底可使用的自行车达到7752辆,求a的值.
a%,三月底可使用的自行车达到7752辆,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
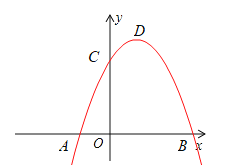
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;(用含有
的坐标为 ;(用含有![]() 的代数式表示)
的代数式表示)
(2)连接![]() .
.
①若![]() 平分
平分![]() ,求二次函数的表达式;
,求二次函数的表达式;
②连接![]() ,若
,若![]() 平分
平分![]() ,求二次函数的表达式.
,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=![]() (x>0)和y=
(x>0)和y=![]() (x<0)的图象分别交于点P,Q.
(x<0)的图象分别交于点P,Q.
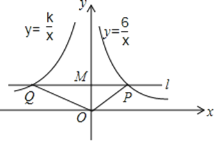
(1)求P点的坐标;
(2)若△POQ的面积为9,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com