
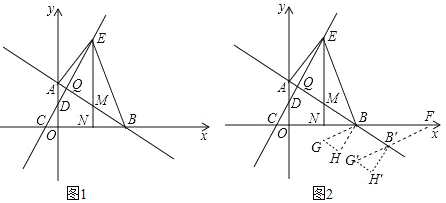
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��AB��y�ύ�ڵ�![]() ����x�ύ�ڵ�B��
����x�ύ�ڵ�B��![]() ��ֱ��CD��y�ύ�ڵ�D����x�ύ�ڵ�
��ֱ��CD��y�ύ�ڵ�D����x�ύ�ڵ�![]() ��
��![]() ��ֱ��AB��ֱ��CD���ڵ�Q��EΪֱ��CD��һ���㣬����E��x��Ĵ��ߣ���ֱ��AB�ڵ�M����x���ڵ�N������AE��BE��
��ֱ��AB��ֱ��CD���ڵ�Q��EΪֱ��CD��һ���㣬����E��x��Ĵ��ߣ���ֱ��AB�ڵ�M����x���ڵ�N������AE��BE��
![]() ��ֱ��AB��CD�Ľ���ʽ����Q�����ꣻ
��ֱ��AB��CD�Ľ���ʽ����Q�����ꣻ
![]() ��E���˶���Q����Ҳ࣬��
��E���˶���Q����Ҳ࣬��![]() �����Ϊ
�����Ϊ![]() ʱ����y������һ����P��ֱ��AB����һ����R����
ʱ����y������һ����P��ֱ��AB����һ����R����![]() ���ܳ���Сʱ�����P�����꼰
���ܳ���Сʱ�����P�����꼰![]() �ܳ�����Сֵ��
�ܳ�����Сֵ��
![]() ��
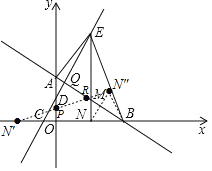
��![]() �ʵ������£���ͼ2��
�ʵ������£���ͼ2��![]() ���ŵ�B��ʱ����ת
���ŵ�B��ʱ����ת![]() �õ�
�õ�![]() ��ʹ��M���G�غϣ���N���H�غϣ��ٽ�
��ʹ��M���G�غϣ���N���H�غϣ��ٽ�![]() ����ֱ��ABƽ�ƣ���ƽ���е�
����ֱ��ABƽ�ƣ���ƽ���е�![]() Ϊ
Ϊ![]() ����ƽ�ƹ����У���ֱ��
����ƽ�ƹ����У���ֱ��![]() ��x�ύ�ڵ�F���Ƿ���������ĵ�F��ʹ��
��x�ύ�ڵ�F���Ƿ���������ĵ�F��ʹ��![]() Ϊ���������Σ������ڣ������ʱ��F�����ꣻ�������ڣ�˵������
Ϊ���������Σ������ڣ������ʱ��F�����ꣻ�������ڣ�˵������
���𰸡���1����Q����Ϊ![]() ����2��
����2��![]() �ܳ�����Сֵ����СֵΪ
�ܳ�����Сֵ����СֵΪ![]() ����3����F������Ϊ
����3����F������Ϊ![]() ��
��
��������
![]() ��ֱ��CD����ʽ��kֵΪ
��ֱ��CD����ʽ��kֵΪ![]() ���������ֱ��CD�ı���ʽ��ͬ���ɵ�ֱ��AB�ı���ʽ��������������ʽ����������Q�����ꣻ
���������ֱ��CD�ı���ʽ��ͬ���ɵ�ֱ��AB�ı���ʽ��������������ʽ����������Q�����ꣻ
![]() �������N���ꣻ��N��������ԳƵ�
�������N���ꣻ��N��������ԳƵ�![]() ��
��![]() ������
������![]() ��AB�ڵ�R��y���ڵ�P����ʱ��
��AB�ڵ�R��y���ڵ�P����ʱ��![]() �ܳ�����Сֵ����⼴�ɣ�
�ܳ�����Сֵ����⼴�ɣ�
![]() �ǵ�Ϊ
�ǵ�Ϊ![]() �ĵ��������Σ�
�ĵ��������Σ�![]() Ϊ���������Σ�������⣮
Ϊ���������Σ�������⣮
![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��CD����ʽ��kֵΪ
��ֱ��CD����ʽ��kֵΪ![]() ��
��
��ֱ��CD�ı���ʽΪ��![]() ������C���������ʽ����ã�
������C���������ʽ����ã�![]() ��
��
�ʣ�ֱ��CD�ı���ʽΪ��![]() ��
��
ͬ���ɵ�ֱ��AB�ı���ʽΪ��![]() ��
��![]() ��
��
����![]() ����ã�
����ã�![]() ������Q����Ϊ
������Q����Ϊ![]() ��
��
![]() ��ͼ��ʾ�����E������Ϊ
��ͼ��ʾ�����E������Ϊ![]() �����
�����![]() ��
��
![]() ��
��
��ã�![]() ������N����Ϊ
������N����Ϊ![]() ����
����![]() ��
��
����N����ֱ��AB��y��ĶԳƵ�![]() ��
��![]() ������
������![]() ��AB�ڵ�R��y���ڵ�P��
��AB�ڵ�R��y���ڵ�P��
��ʱ��![]() �ܳ�����Сֵ����СֵΪ��
�ܳ�����Сֵ����СֵΪ��![]() �ij��ȣ�
�ij��ȣ�
![]() ��
��![]() ����ֱ��AB�Գƣ�
����ֱ��AB�Գƣ�![]() ��
��
![]() Ϊ�߳�Ϊ3�ĵȱ������Σ������θ�Ϊ��
Ϊ�߳�Ϊ3�ĵȱ������Σ������θ�Ϊ��![]() ��
��
���![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��
��ֱ��![]() �ı���ʽΪ��
�ı���ʽΪ��![]() ������P����
������P����![]() ��
��
![]() �ܳ�����Сֵ����СֵΪ
�ܳ�����Сֵ����СֵΪ![]() ��
��
![]() ��ͼ2����
��ͼ2����![]() ���ŵ�B��ʱ����ת
���ŵ�B��ʱ����ת![]() �õ�
�õ�![]() ��
��
��ʱ![]() ������GM����x��Գƣ����
������GM����x��Գƣ����![]() ��
��![]() ��
��
ͼ��ƽ��Ϊ![]() ʱ��
ʱ��![]() ��
��
��![]() �ǵ�Ϊ
�ǵ�Ϊ![]() �ĵ��������Σ���
�ĵ��������Σ���![]() Ϊ���������Σ�ֻ��
Ϊ���������Σ�ֻ��![]() ��
��
![]() ��
��![]() ��
��
�ʵ�F������Ϊ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣�������⣺���֪��![]() ������������������������ѭ��С�������
������������������������ѭ��С�������![]() ��С���������Dz�����ȫ����д��������������1��
��С���������Dz�����ȫ����д��������������1��![]() ��2������
��2������![]() ����������Ϊ1����
����������Ϊ1����![]() ��ȥ����������1�������С������
��ȥ����������1�������С������![]() ���������ϵ����ݣ������������⣺
���������ϵ����ݣ������������⣺
��1��![]() ������������______����������______��
������������______����������______��
��2��![]() ������������______����������_____��
������������______����������_____��
��3������![]() ����������x����������y����x��
����������x��С��������y����x��![]() y��ֵ��
y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ������ƽ���ʽ������ǣ�������
A.��2a+b����2b��a��B.��![]() ��1������
��1������![]() ��1��
��1��
C.��2a��3b������2a+3b��D.����a��2b������a+2b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��֬��˾�������۲����͡�����������ʳ��ֲ���ͣ�
��1����֪�����ij�����Ϊ56%���Dz��ѵ�1.4�������в��ѡ�������100�֣�����õ�����52��ֲ���ͣ������еIJ��������ж��ٶ֣�
��2����ȥ��������У������͡������͵��ۼ۷ֱ�Ϊ20Ԫ/����30Ԫ/������������ͬ���������ڻ���ԭ���ϼ۸����ǣ������͵��ۼ۱�ȥ�������a%�������͵��ۼ۲��䣬��������ȥ�꽵��a%���Ҳ����͡������͵�������ռ������������![]() ��������Ԥ�ƽ���������ܶ��ȥ���½�
��������Ԥ�ƽ���������ܶ��ȥ���½�![]() a%����a��ֵ��
a%����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��D������B��BC�Ĵ��ߣ����Գ����ڵ�E��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��D������B��BC�Ĵ��ߣ����Գ����ڵ�E��

��1����֤����E���D����x��Գƣ�
��2����PΪ���������ڵ��������ϵ�һ���㣬����PAE��������ʱ���ڶԳ�������һ��M����y������һ��N��ʹ��OM+MN+NP��С�����ʱ��M�����꼰OM+MN+NP����Сֵ��
��3����ͼ2��ƽ�������ߣ�ʹ�����ߵĶ���D������AD���ƶ�����Dƽ�ƺ�Ķ�Ӧ��ΪD������A�Ķ�Ӧ��A�����������ߵĶԳ�����x�ύ�ڵ�F������FBC��BC���ۣ�ʹ��F���ڵ�F��������ƽ������һ��G������F����G��D����A��Ϊ������ı���Ϊ���Σ���ƽ�Ƶľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶����������ʵ����ijɼ������������ֳ�5��С�飨x��ʾ�ɼ�����λ���ף���A�飺5.25��x��6.25��B�飺6.25��x��7.25��C�飺7.25��x��8.25��D�飺8.25��x��9.25��E�飺9.25��x��10.25�������Ƴ�����ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������������涨x��6.25Ϊ�ϸ�x��9.25Ϊ���㣮

��1���ⲿ�������ж����ˣ����гɼ��ϸ���ж����ˣ�
��2���ⲿ�������ɼ�����λ��������һ�飿����ͳ��ͼ��D���Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��3��Ҫ�ӳɼ������ѧ���У����ѡ��2�˽��ܾ��飬��֪�ס�����λͬѧ�ijɼ���Ϊ���㣬������������1�˱�ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�ijͬѧ�������ʽ���̵ľ�����̣�
�ⷽ��![]()
�⣺![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����ԭ���̼���֪
����ԭ���̼���֪![]() ��ԭ���̵Ľ⣮
��ԭ���̵Ľ⣮
����ش�
��1���õ���ʽ�������� ��
�õ���ʽ�ľ��������� ��
�õ���ʽ�ľ��������� ��
�õ���ʽ�ĸ����� ��
��2�����������ȷ���������ȷ������һ����ʼ���ִ��� �������ԭ���� ������һ��ش�����ȷ���ģ��˿ղ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��Сѧ����ȫ�ͽ���������ijУ��֯�ˡ�����ˮ����ͨ��ȫ��������֪ʶ������Ϊ�����ھ����б�������İ༶��ѧУ����������Ʒ�̳�һ���Թ������ɸ����������ÿ������ļ۸���ͬ��ÿ������ļ۸���ͬ��������1�������1��������159Ԫ�����������۵�2����9Ԫ��
��1�������������ĵ��۸��Ƕ���Ԫ��
��2������ѧУʵ���������һ���Թ������������20������Ҫ���������������ܷ��ò�����1550Ԫ��ѧУ�����Թ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90������CAD=30����AC=BC=AD��CE��CD����CE=CD������BD��DE��BE�������н��ۣ�����ECA=165������BE=BC����AD��BE����![]() =1��������ȷ���ǣ� ��
=1��������ȷ���ǣ� ��

A���٢ڢ� B���٢ڢ� C���٢ۢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com