练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
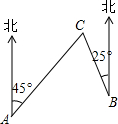
    20．如图，C岛在A岛的北偏东45°方向，C岛在B岛的北偏西25°方向，则从C岛看A、B两岛的视角∠ACB的度数是（　　）
    A．70°B．20°C．35°D．110°

    分析 根据两直线平行，同旁内角互补求得∠C的度数即可．

    解答 解：如图，连接AB，

    ∵两正北方向平行，
    ∴∠CAB+∠CBA=180°-45°-25°=110°，
    ∴∠ACB=180°-110°=70°．
    故选：A．

    点评 本题考查了方向角，解决本题的关键是利用平行线的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．某校举行歌咏比赛，有11名同学参加选拔赛，所得分数各不相同，按成绩取前5名进入决赛，若知道某同学的分数，要判断他能否进入决赛，只需知道这11名同学分数的（　　）
    A．中位数B．平均数C．最高分数D．方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．开封市测得2015年3月22日到29日PM2.5（可入肺颗粒物）的日均值（单位：μg/m3）如下：65，39，52，45，55，71，65，133，这组数据的极差和中位数分别是（　　）
    A．65和60B．65和55C．94和60D．94和55

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，AB∥CD，EF分别交AB、CD与M、N，∠EMB=50°，MG平分∠BMF，MG交CD于G，求∠MGC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

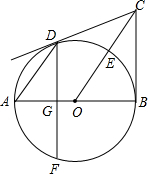    15．如图，AB是⊙O的直径，BC⊥AB于点B，连接OC、BD相交于点E，弦AD∥OC，弦DF⊥AB于点G．
    （1）求证：OC垂直平分BD，
    （2）求证：CD是⊙O的切线；
    （3）若cos∠BAD=$\frac{3}{5}$，⊙O的半径为5，求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知a、b、c分别为Rt△ABC（∠C=90°）的三边的长，则关于x的一元二次方程（c+a）x2+2bx+（c-a）=0根的情况是（　　）
    A．方程无实数根B．方程有两个不相等的实数根
    C．方程有两个相等的实数根D．无法判断

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．新京报讯，2015年全国春运进入节前返程高峰，南京的旅客维持在超过50万人的数量，而全国预计发送旅客突破770万人次，将770万用科学记数法表示为（　　）
    A．77×105B．7.7×106C．7.7×105D．0.77×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．我们规定：线段外一点和这条线段两个端点连线所构成的角叫做这个点对这条线段的视角．如图1，对于线段AB及线段AB外一点C，我们称∠ACB为点C对线段AB的视角．如图2，在平面直角坐标系xoy中，已知点D（0，4），E（0，1）．
    （1）⊙P为过D，E两点的圆，F为⊙P上异于点D，E的一点．
    ①如果DE为⊙P的直径，那么点F对线段DE的视角∠DFE为90度；
    ②如果⊙P的半径为$\sqrt{3}$，那么点F对线段DE的视角∠DFE为60或120度；
    （2）点G为x轴正半轴上的一个动点，当点G对线段DE的视角∠DGE最大时，求点G的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）计算：1007×993
    （2）先化简再求值：2b2+（a+b）（a-b）-（a-b）2，其中a=-3，b=$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案