
分析 (1)先把二次项系数化为1,然后把常数项移到右边;接下来配方,左右两边加上一次项系数一半的平方;左边写成完全平方式;最后直接开方即可;
(2)先把二次项系数化为1,然后把常数项移到右边;接下来配方,左右两边加上一次项系数一半的平方;左边写成完全平方式;最后直接开方即可;
(3)第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可;
(4)先把二次项系数化为1,然后把常数项移到右边;接下来配方,左右两边加上一次项系数一半的平方;左边写成完全平方式;最后直接开方即可;
(5)先把二次项系数化为1,然后把常数项移到右边;接下来配方,左右两边加上一次项系数一半的平方;左边写成完全平方式;最后直接开方即可;
(6)先把二次项系数化为1,然后把常数项移到右边;接下来配方,左右两边加上一次项系数一半的平方;左边写成完全平方式;最后直接开方即可.
解答 解:(1)2x2-4x-2=0;
x2-2x=1,
x2-2x+1=1+1
(x-1)2=2
∴x-1=$±\sqrt{2}$,
∴x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$;
(2)3x2-4x-2=0;
x2-$\frac{4}{3}$x=$\frac{2}{3}$,
x2-$\frac{4}{3}$x+$\frac{4}{9}$=$\frac{2}{3}$+$\frac{4}{9}$
(x-$\frac{2}{3}$)2=$\frac{10}{9}$
∴x-$\frac{2}{3}$=±$\frac{\sqrt{10}}{3}$,
∴x1=$\frac{2+\sqrt{10}}{3}$,x2=$\frac{2-\sqrt{10}}{3}$;
(3)x2-4x-1=0;
x2-4x=1,
x2-4x+4=1+4
(x-2)2=5
∴x-2=±$\sqrt{5}$,
∴x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(4)3x2+$\frac{1}{2}x$-1=0;
x2+$\frac{1}{6}$x=$\frac{1}{3}$,
x2+$\frac{1}{6}$x+$\frac{1}{144}$=$\frac{1}{3}$+$\frac{1}{144}$,
(x+$\frac{1}{12}$)2=$\frac{49}{144}$
∴x+$\frac{1}{12}$=±$\frac{7}{12}$,
∴x1=$\frac{1}{2}$,x2=-$\frac{2}{3}$;
(5)3x2-4x-7=0;
x2-$\frac{4}{3}$x=$\frac{7}{3}$,
x2-$\frac{4}{3}$x+$\frac{4}{9}$=$\frac{7}{3}$+$\frac{4}{9}$,
(x-$\frac{2}{3}$)2=$\frac{25}{9}$
∴x-$\frac{2}{3}$=±$\frac{5}{3}$,
∴x1=$\frac{7}{3}$,x2=-1;
(6)2x2-18=3x.
x2-$\frac{3}{2}$x=9,
x2-$\frac{3}{2}$x+$\frac{9}{16}$=9+$\frac{9}{16}$,
(x-$\frac{3}{4}$)2=$\frac{153}{16}$
∴x-$\frac{3}{4}$=±$\frac{3\sqrt{17}}{4}$,
∴x1=$\frac{3+3\sqrt{17}}{4}$,x2=$\frac{3-3\sqrt{17}}{4}$.
点评 此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用,把左边配成完全平方式,右边化为常数.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
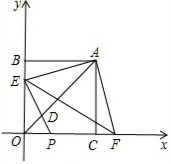 在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,AB⊥y轴于B,AC⊥x轴于C
在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,AB⊥y轴于B,AC⊥x轴于C查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com