
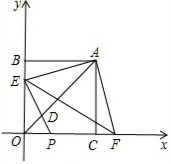
 在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,AB⊥y轴于B,AC⊥x轴于C
在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,AB⊥y轴于B,AC⊥x轴于C分析 (1)根据二次根式有意义的条件确定m的范围,然后去掉绝对值符号,即可求得m的值;
(2)作DG⊥y轴于点G,根据△ODG∽△OAB,根据相似三角形对应边的比相等求得DG的长,则D的坐标即可求得,然后利用待定系数法求得直线EP的解析式,则P的坐标即可求得.
解答 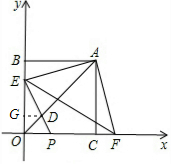 解:(1)根据题意得m-4≥0,则m≥4.则条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,即m-$\sqrt{3}$=m-$\sqrt{m-4}$,
解:(1)根据题意得m-4≥0,则m≥4.则条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,即m-$\sqrt{3}$=m-$\sqrt{m-4}$,
解得:m=7;
(2)作DG⊥y轴于点G.
A的坐标是(7,7),则OA=7$\sqrt{2}$,AB=7,
在直角△ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{7}^{2}+{1}^{2}}$=5$\sqrt{2}$,
则AD=AE=5$\sqrt{2}$,OD=7$\sqrt{2}$-5$\sqrt{2}$=2$\sqrt{2}$.
∵GD∥AB,
∴△ODG∽△OAB,
∴$\frac{DG}{AB}=\frac{OD}{OA}$,即$\frac{DG}{7}=\frac{2\sqrt{2}}{7\sqrt{2}}=\frac{2}{7}$,
则DG=2,
则D的坐标是(2,2).
设ED的解析式是y=kx+b,
则$\left\{\begin{array}{l}{b=6}\\{2k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=6}\\{k=-2}\end{array}\right.$,
则直线EP的解析式是y=-2x+6.
当x=0时,-2x+6=0,解得:x=3.
则P的坐标是(3,0).
点评 本题考查正方形的性质以及相似三角形的判定与性质,正确作出辅助线求得D的坐标是关键.


科目:初中数学 来源: 题型:解答题
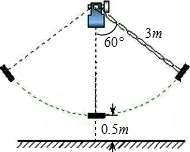 如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?
如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com