
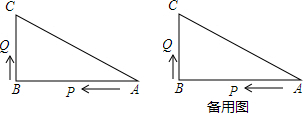
分析 (1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)设出发t秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=2t,BP=8-t,列式求得t即可;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时,则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时,则BC+CQ=12,易求得t;
③当BC=BQ时,过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
解答 解:(1)∵BQ=2×2=4(cm),BP=AB-AP=16-2×1=14(cm ),∠B=90°,
∴PQ=$\sqrt{{4^2}+{{14}^2}}$=$\sqrt{212}$=$2\sqrt{53}$(cm);
(2)BQ=2t,BP=16-t,
根据题意得:2t=16-t,
解得:t=$\frac{16}{3}$,
即出发$\frac{16}{3}$秒钟后,△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,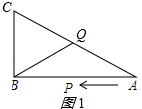
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,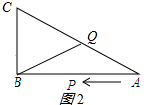
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,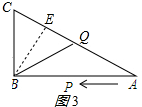
则BE=$\frac{AB•BC}{AC}$=$\frac{12×16}{20}=\frac{48}{5}$,
∴CE=$\sqrt{B{C^2}-B{E^2}}=\sqrt{{{12}^2}-{{(\frac{48}{5})}^2}}=\frac{36}{5}$,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
点评 本题考查了勾股定理、三角形的面积以及等腰三角形的判定和性质,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
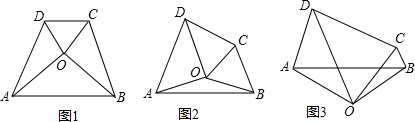
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
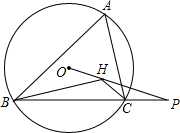 如图所示,已知锐角△ABC的外接圆半径R=1,∠BAC=60°,△ABC的垂心和外心分别为H、O,连接OH、BC交于点P
如图所示,已知锐角△ABC的外接圆半径R=1,∠BAC=60°,△ABC的垂心和外心分别为H、O,连接OH、BC交于点P查看答案和解析>>
科目:初中数学 来源: 题型:解答题
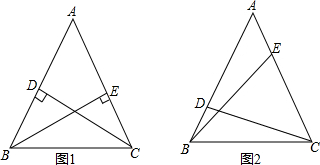
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
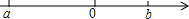 若有理数a,b在数轴上对应的点如图所示,则a、b、-a、-b的大小关系是( )
若有理数a,b在数轴上对应的点如图所示,则a、b、-a、-b的大小关系是( )| A. | a<b<-a<-b | B. | a<-b<b<-a | C. | -b<a<b<-a | D. | -a<-b<a<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
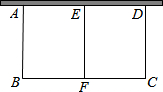 如图所示,已知墙的长度是20米,利用墙的一边,用篱笆围成一个面积为96平方米的长方形ABCD,中间用篱笆分隔出两个小长方形,总共用去36米长的篱笆,求AB的长度?
如图所示,已知墙的长度是20米,利用墙的一边,用篱笆围成一个面积为96平方米的长方形ABCD,中间用篱笆分隔出两个小长方形,总共用去36米长的篱笆,求AB的长度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com