
【题目】如图,东生、夏亮两位同学从学校出发到青年路小学参加现场作文比赛,冬生步行一段时间后,夏亮骑自行车沿相同路线行进,两人都是匀速前进,他们的路程差s(米)与冬生出发时间t(分)之间的函数关系如图所示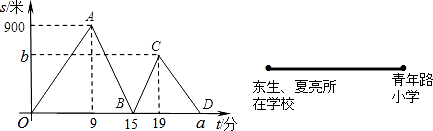
(提示:先根据图象还原东生、夏亮的行走过程,特别注意s代表的是两人的路程差)根据图象进行以下探究:
(1)冬生的速度是米/分,请你解释点B坐标(15,0)所表示的意义:;
(2)求夏亮的速度和他们所在学校与青年路小学的距离;
(3)求a,b值;
(4)线段CD对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
【答案】
(1)100;夏亮骑车追上冬生
(2)
解:由题意和图象可得,
夏亮的速度是:15×100÷(15﹣9)=250米/秒,
他们所在学校与青年路小学的距离是:250×(19﹣9)=2500米,
即夏亮的速度是250米/秒,他们所在学校与青年路小学的距离是2500米;
(3)
解:a=2500÷100=25,
b=2500﹣100×19=600,
即a的值是25,b的值是600;
(4)
解:设过点C(19,600),点D(25,0)的直线的解析式为y=kx+b,
![]() ,
,
解得, ![]() ,
,
即y=﹣100x+2500,
线段CD对应的一次函数表达式中,一次项系数是﹣100,它的实际意义是冬生的步行速度.
【解析】解:(1)由题意可得,
冬生的速度为;900÷9=100米/秒,点B坐标(15,0)所表示的意义夏亮骑车追上冬生,
所以答案是:100,夏亮骑车追上冬生;


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°.
(1)作∠A的平分线AD,交BC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加黑);
(2)计算S△DAC:S△ABC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
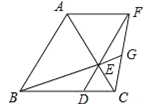
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图.请根据图中所给的信息解答下列问题: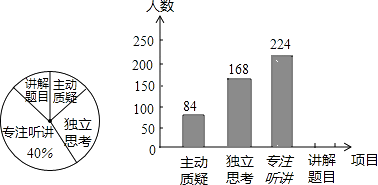
(1)这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC. 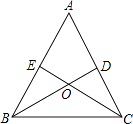
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com