
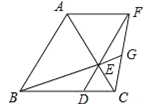
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①正确.∵△ABC是等边三角形,∴AB=AC=BC,∠BAC=∠ACB=60°,∵DE=DC,∴△DEC是等边三角形,∴ED=EC=DC,∠DEC=∠AEF=60°,∵EF=AE,∴△AEF是等边三角形,∴AF=AE,∠EAF=60°,在△ABE和△ACF中,∵AB=AC,∠BAE=∠CAF,AE=AF,∴△ABE≌△ACF,故①正确.
②正确.∵∠ABC=∠FDC,∴AB∥DF,∵∠EAF=∠ACB=60°,∴AB∥AF,∴四边形ABDF是平行四边形,∴DF=AB=BC,故②正确.
③正确.∵△ABE≌△ACF,∴BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,∵BC=DF,CE=CD,BE=CF,∴△BCE≌△FDC,∴S△BCE=S△FDC,∴S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.
④正确.∵△BCE≌△FDC,∴∠DBE=∠EFG,∵∠BED=∠FEG,∴△BDE∽△FGE,∴![]() ,∴
,∴![]() =
=![]() ,∵BD=2DC,DC=DE,∴
,∵BD=2DC,DC=DE,∴![]() =2,∴FG=2EG.故④正确.
=2,∴FG=2EG.故④正确.
综上所述:①②③④正确.故答案为:①②③④.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b中,k<0,b<0,则函数不经过下列选项中的那个象限( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1:y1=x1+2和直线l2:y2=﹣x2+4相交于点A,分别于x轴相交于点B和点C,分别与y轴相交于点D和点E.
(1)在平面直角坐标系中按照列表、描点、连线的方法画出直线l1和l2的图象,并写出A点的坐标.
(2)求△ABC的面积.
(3)求四边形ADOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果线段AB=5cm,BC=4cm,且A,B,C,D,在同一条直线上,那么A,C两点的距离是( )
A.1cm
B.9cm
C.1cm或9cm
D.以上答案都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,东生、夏亮两位同学从学校出发到青年路小学参加现场作文比赛,冬生步行一段时间后,夏亮骑自行车沿相同路线行进,两人都是匀速前进,他们的路程差s(米)与冬生出发时间t(分)之间的函数关系如图所示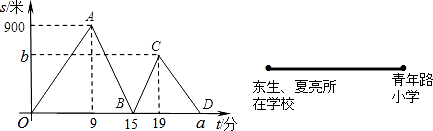
(提示:先根据图象还原东生、夏亮的行走过程,特别注意s代表的是两人的路程差)根据图象进行以下探究:
(1)冬生的速度是米/分,请你解释点B坐标(15,0)所表示的意义:;
(2)求夏亮的速度和他们所在学校与青年路小学的距离;
(3)求a,b值;
(4)线段CD对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
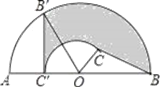
【题目】如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为______cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com