
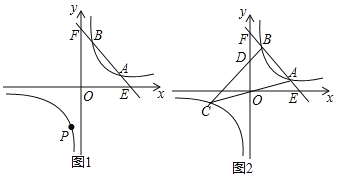
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】(1)![]() ,B(1,8);(2)(﹣4,﹣2)、(﹣16,
,B(1,8);(2)(﹣4,﹣2)、(﹣16,![]() );(3)10.
);(3)10.
【解析】
试题(1)把点A的坐标代入![]() ,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;
,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;
(2)△PAB是以AB为直角边的直角三角形,分两种情况讨论:①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,求得OE=5,OH=4,AH=2,HE=1.证明△AHM∽△EHA,再根据相似三角形的性质可求出MH,从而得到点M的坐标,然后用待定系数法求出直线AP的解析式,再解直线AP与反比例函数的解析式组成的方程组,就可得到点P的坐标;②若∠ABP=90°,同理即可得到点P的坐标;
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,易证△CTD∽△BSD,根据相似三角形的性质可得![]() .由A(a,﹣2a+10),B(b,﹣2b+10),可得C(﹣a,2a﹣10),CT=a,BS=b,即可得到
.由A(a,﹣2a+10),B(b,﹣2b+10),可得C(﹣a,2a﹣10),CT=a,BS=b,即可得到![]() .由A、B都在反比例函数的图象上可得a(﹣2a+10)=b(﹣2b+10),把
.由A、B都在反比例函数的图象上可得a(﹣2a+10)=b(﹣2b+10),把![]() 代入即可求出a的值,从而得到点A、B、C的坐标,运用待定系数法求出直线BC的解析式,从而得到点D的坐标及OD的值,然后运用割补法可求出S△COB,再由OA=OC可得S△ABC=2S△COB.
代入即可求出a的值,从而得到点A、B、C的坐标,运用待定系数法求出直线BC的解析式,从而得到点D的坐标及OD的值,然后运用割补法可求出S△COB,再由OA=OC可得S△ABC=2S△COB.
试题解析:(1)把A(4,2)代入![]() ,得k=4×2=8,∴反比例函数的解析式为
,得k=4×2=8,∴反比例函数的解析式为![]() ,解方程组
,解方程组 ,得:
,得:![]() 或
或![]() ,∴点B的坐标为(1,8);
,∴点B的坐标为(1,8);
(2)①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=﹣2x+10,当y=0时,﹣2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5﹣4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴![]() ,∴
,∴![]() ,∴MH=4,∴M(0,0),可设直线AP的解析式为
,∴MH=4,∴M(0,0),可设直线AP的解析式为![]() ,则有
,则有![]() ,解得m=
,解得m=![]() ,∴直线AP的解析式为
,∴直线AP的解析式为![]() ,解方程组
,解方程组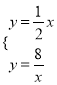 ,得:
,得:![]() 或
或![]() ,∴点P的坐标为(﹣4,﹣2).
,∴点P的坐标为(﹣4,﹣2).
②若∠ABP=90°,同理可得:点P的坐标为(﹣16,![]() ).
).
综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,![]() );
);
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,则有BS∥CT,∴△CTD∽△BSD,∴![]() .∵
.∵![]() ,∴
,∴![]() .∵A(a,﹣2a+10),B(b,﹣2b+10),∴C(﹣a,2a﹣10),CT=a,BS=b,∴
.∵A(a,﹣2a+10),B(b,﹣2b+10),∴C(﹣a,2a﹣10),CT=a,BS=b,∴![]() =
=![]() ,即
,即![]() .∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数
.∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数![]() 的图象上,∴a(﹣2a+10)=b(﹣2b+10),∴a(﹣2a+10)=
的图象上,∴a(﹣2a+10)=b(﹣2b+10),∴a(﹣2a+10)=![]() (﹣2×
(﹣2×![]() +10).∵a≠0,∴﹣2a+10=
+10).∵a≠0,∴﹣2a+10=![]() (﹣2×
(﹣2×![]() +10),解得:a=3.∴A(3,4),B(2,6),C(﹣3,﹣4).
+10),解得:a=3.∴A(3,4),B(2,6),C(﹣3,﹣4).
设直线BC的解析式为![]() ,则有
,则有![]() ,解得:
,解得:![]() ,∴直线BC的解析式为
,∴直线BC的解析式为![]() .当x=0时,y=2,则点D(0,2),OD=2,∴S△COB=S△ODC+S△ODB=
.当x=0时,y=2,则点D(0,2),OD=2,∴S△COB=S△ODC+S△ODB=![]() OD·CT+
OD·CT+![]() OD·BS=
OD·BS=![]() ×2×3+
×2×3+![]() ×2×2=5.∵OA=OC,∴S△AOB=S△COB,∴S△ABC=2S△COB=10.
×2×2=5.∵OA=OC,∴S△AOB=S△COB,∴S△ABC=2S△COB=10.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】(发现)x4﹣5x2+4=0是一个一元四次方程.
(探索)根据该方程的特点,通常用“换元法”解方程:
设x2=y,那么x4= ,于是原方程可变为 .
解得:y1=1,y2= .
当y=1时,x2=1,∴x=±1;
当y= 时,x2= ,∴x= ;
原方程有4个根,分别是 .
(应用)仿照上面的解题过程,求解方程:(x2﹣2x)2+(x2﹣2x)﹣6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
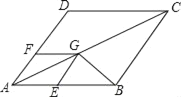
【题目】如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
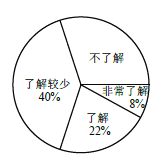
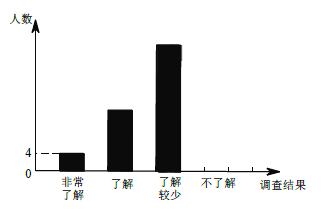
(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
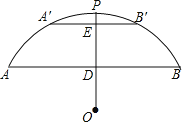
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
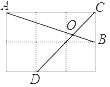
A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com