
【题目】如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
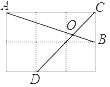
A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
科目:初中数学 来源: 题型:
【题目】知识背景
当a>0且x>0时,因为(![]() ﹣
﹣![]() )2≥0,所以x﹣2
)2≥0,所以x﹣2![]() +
+![]() ≥0,从而x+
≥0,从而x+![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数y=x+![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=![]() 时,该函数有最小值为2
时,该函数有最小值为2![]() .
.
应用举例
已知函数为y1=x(x>0)与函数y2=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,y1+y2=x+
=2时,y1+y2=x+![]() 有最小值为2
有最小值为2![]() =4.
=4.
解决问题
(1)已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )
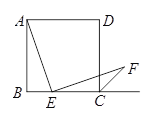
A. 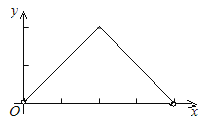 B.
B. 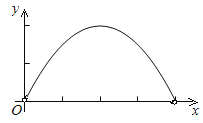
C. 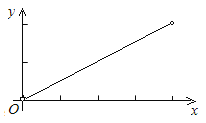 D.
D. 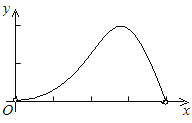
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
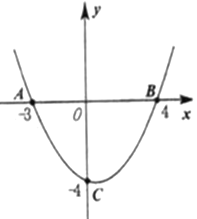
(1)求抛物线解析式:
(2)抛物线对称轴上存在一点![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 值最大时,求点H坐标:
值最大时,求点H坐标:
(3)若抛物线上存在一点![]() ,
,![]() ,当
,当![]() 时,求点
时,求点![]() 坐标:
坐标:
(4)若点M是![]() 平分线上的一点,点
平分线上的一点,点![]() 是平面内一点,若以
是平面内一点,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形,请直接写出点
为顶点的四边形是矩形,请直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
(1)求一次函数与反比例函数的表达式;
(2)当x>0时,比较kx+b与![]() 的大小.
的大小.
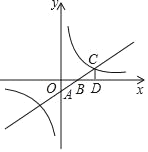
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏学习之余设计了一个求函数表达式的程序,具体如图所示,则当输入下列点的坐标时,请按程序指令解答.
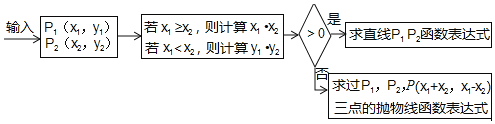
(1)P1(1,0),P2(﹣3,0).
(2)P1(2,﹣1),P2(4,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
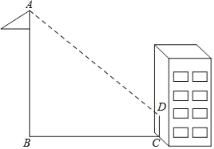
【题目】数学兴趣小组的同学们,想利用自己所学的数学知识测量学校旗杆的高度:下午活动时间,兴趣小组的同学们来到操场,发现旗杆的影子有一部分落在了墙上(如图所示).同学们按照以下步骤进行测量:测得小明的身高1.65米,此时其影长为2.5米;在同一时刻测量旗杆影子落在地面上的影长BC为9米,留在墙上的影高CD为2米,请你帮助兴趣小组的同学们计算旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com