
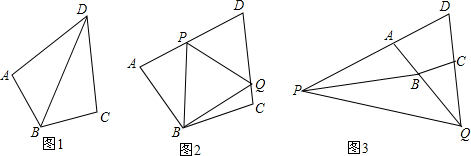
分析 (1)如图1,利用HL证得两个直角三角形全等:Rt△BAD≌Rt△BCD,则其对应边相等:AD=DC=2;
(2)如图2,延长DC,在上面找一点K,使得CK=AP,连接BK,通过证△BPA≌△BCK(SAS)得到:∠1=∠2,BP=BK.然后由全等三角形△PBQ≌△BKQ的徐表格中求得∠PBQ=$\frac{1}{2}$∠ABC,结合已知条件“∠ABC+∠ADC=180°”可以推知∠PBQ=90°-$\frac{1}{2}$∠ADC;
(3)(2)中结论不成立,应该是:∠PBQ=90°+$\frac{1}{2}$∠ADC.
如图3,在CD延长线上找一点K,使得KC=AP,连接BK,构建全等三角形:△BPA≌△BCK(SAS),由该全等三角形的性质和全等三角形的判定定理SSS证得:△PBQ≌△BKQ,则其对应角相等:∠PBQ=∠KBQ,结合四边形的内角和是360度可以推得:∠PBQ=90°+$\frac{1}{2}$∠ADC.
解答 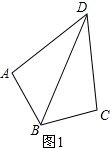 (1)解:如图1,∵∠ABC+∠ADC=180°,∠BAD=90°,
(1)解:如图1,∵∠ABC+∠ADC=180°,∠BAD=90°,
∴∠BCD=90°,
在Rt△BAD和Rt△BCD中,
$\left\{\begin{array}{l}{BD=BD}\\{AB=BC}\end{array}\right.$,
∴Rt△BAD≌Rt△BCD(HL),
∴AD=DC=2,
∴DC=2;
(2)如图2,延长DC,在上面找一点K,使得CK=AP,连接BK,
∵∠ABC+∠ADC=180°,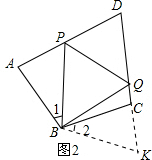
∴∠BAD+∠BCD=180°.
∵∠BCD+∠BCK=180°,
∴∠BAD=∠BCK,
在△BPA和△BCK中,
$\left\{\begin{array}{l}{AP=CK}\\{∠BAP=∠BCK}\\{AB=BC}\end{array}\right.$,
∴△BPA≌△BCK(SAS),
∴∠1=∠2,BP=BK.
∵PQ=AP+CQ,
∴PQ=QK,
∵在△PBQ和△BKQ中,
$\left\{\begin{array}{l}{BP=BK}\\{BQ=BQ}\\{PQ=KQ}\end{array}\right.$,
∴△PBQ≌△BKQ(SSS),
∴∠PBQ=∠KBQ,
∴∠PBQ=∠2+∠CBQ=∠1+∠CBQ,
∴∠PBQ=$\frac{1}{2}$∠ABC.
∵∠ABC+∠ADC=180°,
∴∠ABC=180°-∠ADC,
∴$\frac{1}{2}$∠ABC=90°-$\frac{1}{2}$∠ADC,
∴∠PBQ=90°-$\frac{1}{2}$∠ADC;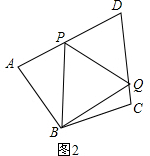
(3)(2)中结论不成立,应该是:∠PBQ=90°+$\frac{1}{2}$∠ADC.
如图3,在CD延长线上找一点K,使得KC=AP,连接BK,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°.
∵∠BAD+∠PAB=180°,
∴∠PAB=∠BCK.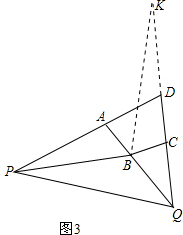
在△BPA和△BCK中,
$\left\{\begin{array}{l}{AP=CK}\\{∠BAP=∠BCK}\\{AB=BC}\end{array}\right.$,
∴△BPA≌△BCK(SAS),
∴∠ABP=∠CBK,BP=BK,
∴∠PBK=∠ABC.
∵PQ=AP+CQ,
∴PQ=QK,
在△PBQ和△BKQ中,
$\left\{\begin{array}{l}{BP=BK}\\{BQ=BQ}\\{PQ=KQ}\end{array}\right.$,
∴△PBQ≌△BKQ(SSS),
∴∠PBQ=∠KBQ,
∴2∠PBQ+∠PBK=2∠PBQ+∠ABC=360°,
∴2∠PBQ+(180°-∠ADC)=360°,
∴∠PBQ=90°+$\frac{1}{2}$∠ADC.
点评 本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
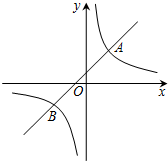 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com