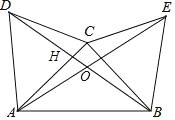
【题目】如图，在△ABC中，分别以AC、BC为边作等边三角形ACD和等边三角形BCE，连接AE、BD交于点O．
（1）求证：△ACE≌△DCB；
（2）求∠AOB的度数．
【答案】（1）证明见解析；（2）120°.
【解析】
(1)已知三角形ACD，三角形BCE是等边三角形，可求出∠DCB=∠ACE，随之利用SAS可证明全等.
(2)利用第一问结果得出∠AOH=∠DCH=60°，随之可求∠AOB的度数.
证明：（1）如图：AC与BD交于点H．
∵△ACD，△BCE都是等边三角形，
∴CD=CA，CB=CE，∠ACD=∠BCE=60°，
∴∠DCB=∠ACE，
在△DCB和△ACE中，
，
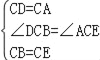∴△DCB≌△ACE（SAS），
（2）∵△DCB≌△ACE，
∴∠CAE=∠CDB，
∵∠DCH+∠CHD+∠BDC=180°，∠AOH+∠AHO+∠CAE=180°，∠DHC=∠OHA，
∴∠AOH=∠DCH=60°，
∴∠AOB=180°﹣∠AOH=120°．
科目：初中数学 来源： 题型：
【题目】如图，在锐角△ABC中，AC是最短边．以AC为直径的⊙O，交BC于D，过O作OE∥BC，交OD于E，连接AD、AE、CE．
（1）求证：∠ACE=∠DCE；
（2）若∠B=45°，∠BAE=15°，求∠EAO的度数；
（3）若AC=4，
，求CF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△DEB中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是
A．BC=EC，∠B=∠E B．BC=EC，AC=DC
C．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，点E在BC上．过点D作DF∥BC，连接DB．
求证：（1）△ABD≌△ACE；
（2）DF=CE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上．
（1）如图1，当点E在边BC上时，求证DE＝EB；
（2）如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；
（3）如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3．求CG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：一组数据x1，x2，x3，x4，x5的平均数是2，方差是
，那么另一组数据3x1﹣2，3x2﹣2，3x3﹣2，3x4﹣2，3x5﹣2的平均数和方差分别是（ ）
A. 2， B. 4，3 C. 4，
D. 2，1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下题的解答过程，然后解答后面的问题，
已知多项式2x3﹣x2+m有一个因式是2x+1，求m的值
解法一：设2x3﹣x2+m＝x+m＝（2x+1）（x2+ax+b）
则2x3﹣x2+m＝2x3+（2a+1）x2+（a+2b）x+b
比较系数得
，解得
∴m＝
．
解法二：设2x3﹣x2+m＝A（2x+1）（A为整式）
由于上式为恒等式，为方便计算取x＝
，
，故m＝
选择恰当的方法解答下列各题
（1）已知关于的多项式x2+mx﹣15有一个因式是x﹣3，m＝ ．
（2）已知x4+mx3+nx﹣16有因式（x﹣1）和（x﹣2），求m、n的值：
（3）已知x2+2x+1是多项式x3﹣x2+ax+b的一个因式，求a，b的值，并将该多项式分解因式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD平分∠BAC，EG⊥AD，分别交AB，AD，AC，BC的延长线于E，H，F，G
已知四个式子：①∠1＝
(∠2＋∠3)；②∠1＝(∠3－∠2)；③∠4＝ (∠3－∠2)；④∠4＝∠1．其中正确的式子有______．(填写序号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方体的长为15厘米，宽为10厘米，高为20厘米，点B到点C的距离是5厘米.
（1）通过计算，一只小虫在长方体表面从A爬到B的最短路程是多少？
（2）在此长方体盒子内放入一根木棒，木棒的最大长度是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com