
【题目】如图,△ABC中,AD平分∠BAC,EG⊥AD,分别交AB,AD,AC,BC的延长线于E,H,F,G

已知四个式子:①∠1=![]() (∠2+∠3);②∠1=
(∠2+∠3);②∠1=![]() (∠3-∠2);③∠4=
(∠3-∠2);③∠4=![]() (∠3-∠2);④∠4=
(∠3-∠2);④∠4=![]() ∠1.其中正确的式子有______.(填写序号)
∠1.其中正确的式子有______.(填写序号)
【答案】①③.
【解析】
由AD平分∠BAC,EG⊥AD,根据三角形的内角和定理得∴∠1=90°-∠BAD=90°-![]() ∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°-
∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°-![]() (180°-∠2-∠3)=
(180°-∠2-∠3)=![]() (∠2+∠3)故①正确;再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2=
(∠2+∠3)故①正确;再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2=![]() (∠2+∠3)-∠2=
(∠2+∠3)-∠2=![]() (∠3-∠2),故③正确;根据三角形内角和定理得到∠1=∠AFH,然后可得∠3=∠4+∠1,结合∠1=∠4+∠2可得
(∠3-∠2),故③正确;根据三角形内角和定理得到∠1=∠AFH,然后可得∠3=∠4+∠1,结合∠1=∠4+∠2可得![]() (∠3-∠2)=∠4,然后可得②错误;根据∠1=∠2+∠4,∠2和∠4不一定相等,可得④错误,由此得到正确答案.
(∠3-∠2)=∠4,然后可得②错误;根据∠1=∠2+∠4,∠2和∠4不一定相等,可得④错误,由此得到正确答案.
解:∵AD平分∠BAC,EG⊥AD,
∴∠BAD=∠CAD =![]() ∠BAC,∠AMF=∠ANE=90°,
∠BAC,∠AMF=∠ANE=90°,
∴∠1=90°-∠BAD=90°-![]() ∠BAC,
∠BAC,
而∠BAC=180°-∠2-∠3,
∴∠1=90°-![]() (180°-∠2-∠3)=
(180°-∠2-∠3)=![]() (∠2+∠3),故①正确;
(∠2+∠3),故①正确;
又∵∠1=∠2+∠4,
∴∠4=∠1-∠2=![]() (∠2+∠3)-∠2=
(∠2+∠3)-∠2=![]() (∠3-∠2),故③正确;
(∠3-∠2),故③正确;
∵∠1+∠BAD+∠AHE=180°,∠AFH+∠CAD+∠AHF=180°,
∴∠1=∠AFH,
∴∠3=∠4+∠CFG=∠4+∠AFH=∠4+∠1,
∴∠3-∠2=∠4+∠1-∠2
∵∠1=∠4+∠2,
∴∠3-∠2=2∠4,
∴![]() (∠3-∠2)=∠4,
(∠3-∠2)=∠4,
∴∠1=![]() (∠3-∠2)错误,即②错误;
(∠3-∠2)错误,即②错误;
∵∠1=∠2+∠4,∠2和∠4不一定相等,
∴∠4=![]() ∠1错误,即④错误.
∠1错误,即④错误.
故答案为:①③.


科目:初中数学 来源: 题型:
【题目】如图,直线OD与x轴所夹的锐角为30°,OA1的长为2,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三边形,点A1、A2、A3…An﹣1在x轴正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点B2的坐标为____,点Bn的坐标为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O.
(1)求证:△ACE≌△DCB;
(2)求∠AOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点A′的坐标(____________),顶点B的坐标(____________),顶点C关于原点对称的点C′的坐标(____________).
(2)△ABC的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一透明圆柱形无盖容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时一只蚂蚁在杯外壁底部与蜂蜜相对的A处.

(1)若蜂蜜固定不动,求蚂蚁吃到蜂蜜所爬行的最短路线长;
(2)若该蚂蚁刚出发时发现B处的蜂蜜正以0.5cm/s的速度沿杯内壁下滑,它便沿最短路径在8秒钟时吃到了蜂蜜,求此蚂蚁爬行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
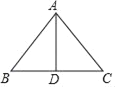
【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,将此等腰三角形纸片沿底边BC上的高AD剪成两个全等的三角形,用这两个三角形拼成一个平行四边形,则所拼出的所有平行四边形中最长的对角线的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:![]() =___________,
=___________,![]() =___________,
=___________,![]() =___________,
=___________,
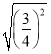 =_________,
=_________,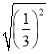 =__________,
=__________,![]() =___________,
=___________,
根据计算结果,回答:
(1)![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请你用数学语言描述出来。
吗?你发现其中的规律了吗?请你用数学语言描述出来。
(2)利用你总结的规律,计算:
①若![]() ,则
,则![]() =_____________;
=_____________;
②![]() =______________________;
=______________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com