
【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米.
(1)通过计算,一只小虫在长方体表面从A爬到B的最短路程是多少?
(2)在此长方体盒子内放入一根木棒,木棒的最大长度是多少?

【答案】(1)25厘米;(2)![]() 厘米
厘米
【解析】
(1)求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.
(2)利用长方体的性质,根据勾股定理解答即可.
解:(1)把长方体的右侧表面展开与前面这个侧面所在的平面形成一个长方形,如图1:
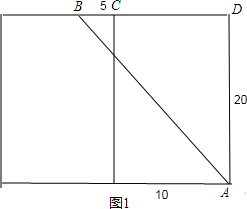
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB=![]() =
=![]() =25cm;
=25cm;
把长方体的右侧表面展开与上面这个侧面所在的平面形成一个长方形,如图2:
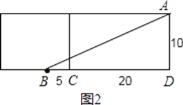
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB=![]() =
=![]() =5
=5![]() cm;
cm;
把长方体的上面表面展开与后面这个侧面所在的平面形成一个长方形,如图3:
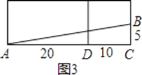
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB=![]() =
=![]() =5
=5![]() cm;
cm;
∵25<5![]() <5
<5![]() ,
,
∴自A至B在长方体表面的连线距离最短是25cm.
故答案为:25厘米;
(2)连接AE,EG,
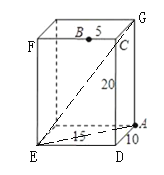
在Rt△ADE中,AD=10cm,ED=15cm,由勾股定理得,
AE=![]() =
=![]() =5
=5![]() cm,
cm,
在Rt△AEG中,AE=5![]() cm,AG=20cm,
cm,AG=20cm,
由勾股定理得,EG=![]() =
=![]() =5
=5![]() cm.
cm.
即木棒的最大长度是5![]() 厘米.
厘米.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O.
(1)求证:△ACE≌△DCB;
(2)求∠AOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:![]() =___________,
=___________,![]() =___________,
=___________,![]() =___________,
=___________,
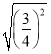 =_________,
=_________,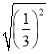 =__________,
=__________,![]() =___________,
=___________,
根据计算结果,回答:
(1)![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请你用数学语言描述出来。
吗?你发现其中的规律了吗?请你用数学语言描述出来。
(2)利用你总结的规律,计算:
①若![]() ,则
,则![]() =_____________;
=_____________;
②![]() =______________________;
=______________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示a,点B表示b,且a,b满足![]()
(1)x表示a+b的整数部分,y表示a+b的小数部分,则x= y = ;
(2)若点A与点C之间的距离表示AC,点B与点C之间的距离表示BC,请在数轴上找一点C,使得AC=2BC,求点C在数轴上表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数![]() (k,b为常数),下表中给出5组自变量及其对应的函数值:
(k,b为常数),下表中给出5组自变量及其对应的函数值:
| …… | -1 | 0 | 1 | 2 | 3 | |
| …… | -2 | 1 | 4 | 8 | 10 | …… |
其中只有1个函数值计算有误,则这个错误的函数值是( )
A.1B.4C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F.

(1)求证:△DAC≌△EAB.
(2)求证:CD⊥BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com