
【题目】在我市“青山绿水”行动中,某村计划对面积为3640![]() 的山坡进行绿化,经投标由甲,乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天完能完成绿化的面积的2倍,如果两队各自独立完成面积为400
的山坡进行绿化,经投标由甲,乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天完能完成绿化的面积的2倍,如果两队各自独立完成面积为400![]() 区域的绿化时,甲队比乙队少用4天.
区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,该村要使这次绿化的总费用不过40万元,则至少应安排乙工程队绿化多少天?
【答案】(1)甲队每天能完成的绿化面积为100m2, 乙队每天能完成的绿化面积为50m2.(2)至少应安排乙工程队绿化37天.
【解析】
(1)设乙工程队每天能完成绿化的面积是xm2,根据题意列出方程,求解即可;
(2)设甲工程队施工a天,乙工程队施工b天刚好完成绿化任务,由题意得:100a+50b=3640,则a=![]() ,根据题意得出1.2×
,根据题意得出1.2×![]() +0.5b≤40,解不等式即可.
+0.5b≤40,解不等式即可.
解.(1)设乙队每天能完成的绿化面积为xm2,则甲队每天能完成的绿化面积为2xm2,
根据题意得![]() ,
,
解得![]() ,
,
经检验:x=50是原方程的解,则2x=100,
答:甲队每天能完成的绿化面积为100m2, 乙队每天能完成的绿化面积为50m2;
(2)设甲工程队施工a天,乙工程队施工b天刚好完成绿化任务,由题意得:
100a+50b=3640,
则a=![]() ,
,
根据题意得:1.2×![]() +0.5b≤40,
+0.5b≤40,
解得:b≥![]() ,
,
答:至少应安排乙工程队绿化37天.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c和直线y=kx+b都经过点(﹣1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )
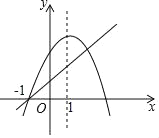
A.ac>0
B.b2﹣4ac<0
C.k=2a+c
D.x=4是ax2+(b﹣k)x+c<b的解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为_____.
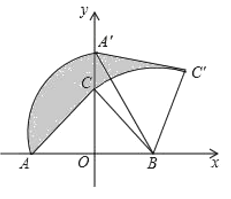
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学决定开展课后服务活动,学校就“你最想开展哪种课后服务项目”问题进行了随机问卷调查,调查分为四个类别:![]() .舞蹈;
.舞蹈;![]() .绘画与书法;
.绘画与书法;![]() .球类;
.球类;![]() .不想参加.现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.不想参加.现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
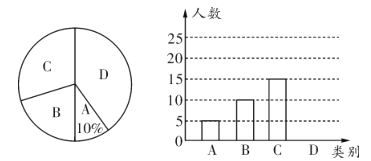
(1)这次统计共抽查了_________名学生,请补全条形统计图;
(2)该校共有600名学生,根据以上信息,请你估计全校学生中想参加![]() 类活动的人数;
类活动的人数;
(3)若甲、乙两名同学,各自从![]() 三个项目中随机选一个参加,请用列表或画树状图的方法求他们选中同一项目的概率.
三个项目中随机选一个参加,请用列表或画树状图的方法求他们选中同一项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数ymxn与反比例函数y![]() 同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
(1)判断y2x1与y![]() 是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
(2)已知:整数m,n,t满足条件t<n<8m,并且一次函数y=(1+n)x+2m+2与反比例函数y![]() 存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
(3)若一次函数yxm和反比例函数y![]() 在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批学习笔记本,已知1本甲种笔记本和3本乙种笔记本共需26元;3本甲种笔记本和2本乙种笔记本共需29元.
(1)求购买一本甲种笔记本和一本乙种笔记本各需多少元;
(2)学校计划购进这两种笔记本共70本,并且甲种笔记本的数量不超过乙种笔记本数量的2倍,若设学校计划购进甲种比价本x本.
①填写下表:
甲种笔记本数量 | 10 |
|
乙种笔记本数量 |
| 30 |
所需总费用 |
|
|
②写出购买这两种笔记本所需要费用y(元)关于x的函数关系式;请设计出最省钱的购买方案,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com