
【题目】用正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需______个长方形,______个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
现有相同规格的 19 张正方形硬纸板,其中的 x 张按方法一裁剪,剩余的按方法二裁剪.
①用含 x 的代数式分别表示裁剪出的侧面个数,底面个数;
②若裁剪出的侧面和底面恰好全部用完,求能做多少个盒子.

【答案】(1)3,2;(2)30个
【解析】试题分析:(1)由图可知每个三棱柱盒子需3个长方形,2个等边三角形;
(2)①由![]() 张用A方法,就有
张用A方法,就有![]() 张用B方法,就可以分别表示出侧面个数和底面个数;
张用B方法,就可以分别表示出侧面个数和底面个数;
②由侧面个数和底面个数比为3:2建立方程求出![]() 的值,求出侧面的总数就可以求出结论.
的值,求出侧面的总数就可以求出结论.
试题解析:(1)由图可知每个三棱柱盒子需3个长方形,2个等边三角形;
(2)①∵裁剪时x张用A方法,
∴裁剪时(19x)张用B方法,
∴侧面的个数为:6x+4(19x)=(2x+76)个,
底面的个数为:5(19x)=(955x)个;
②由题意,得![]()
解得:x=7,
经检验,x=7是原分式方程的解,
∴盒子的个数为: ![]()
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
故答案为3,2.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1).
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )
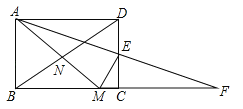
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据本校的实际情况,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.规定每个学生必须参加一项活动.学校为了了解学生最喜欢哪一种项目,拟采用以下的方式进行调查.
方式一:调查该校七年级女生喜欢的运动项目
方式二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方式三:调查该校书法小组的学生喜欢的运动项目
方式四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方式合适的是 ;
学校体育组采用了(1)中的方式,将调查的结果绘制成右侧两幅不完整的统计图.请你结合图中的信息解答下列问题:
(2)在扇形统计图中,B 项目对应的圆心角的度数为 ;
(3)请补全条形统计图;
(4)已知该校有 3600 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图表是 2017 年某校从参加中考体育测试的九年级学生中随机调查的 10 名男生跑 1000 米和 10 名女生跑 800米的成绩.

(1) 按规定,女生跑 800 米的时间不超过 3'24"就可以得满分.该校九年级学生有 490 人,男生比女生少 70 人.请你根据上面成绩,估计该校女生中有多少人该项测试成绩得满分?
(2) 假如男生 1 号和男生 10 号被分在同组测试,请分析他俩在 400 米的环形跑道测试的过程中能否相遇。 若能,求出发多长时间才能相遇;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com