
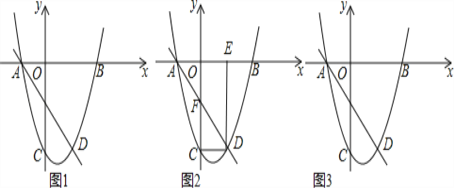
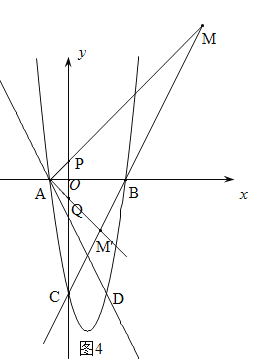
【题目】如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6).
(1)求抛物线的解析式;
(2)如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(3)如果点M是直线BC上的动点,是否存在一个点M,使△ABM中有一个角为45°?如果存在,直接写出所有满足条件的M点坐标;如果不存在,请说明理由.
【答案】(1)y=2x2﹣4x﹣6(2)当t=2时,有PQ⊥DF(3)点M(7,8),(![]() ,
,![]() ),(
),( ![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
【解析】试题分析:(1)求出点A坐标,把A、B、C三点代入抛物线解析式解方程组即可.
(2)分三种情形讨论①当Q点在CD上时②点Q在CO上时③点Q在OE上时,利用相似三角形的性质路程方程求出t,并且判断是否符合题意即可.
(3)分三种情况:①当∠MAB=45°且M在x轴上方时,则直线过A和P(0, 1),求出直线AP的解析式和直线AP与直线BC的交点即可;
②当∠MAB=45°且M在x轴下方时,则直线过A和Q(0,-1),类似可求M的坐标;
③若∠AMB=45°,过A作AP⊥BC于P,则△APM是等腰直角三角形,得到AP=PM.求出直线AP的解析式,然后求出直线AP和直线CB的交点P的坐标,由MP=AP,用两点间的距离公式,列方程求解即可.
试题解析:解:(1)令y=0,则﹣2x﹣2=0,解得:x=﹣1,所以点A坐标(﹣1,0),设抛物线解析式为y=ax2+bx+c.∵A(﹣1,0)、B(3,0)、C(0,﹣6)在抛物线上,∴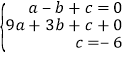 ,解得:
,解得: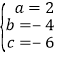 ,∴抛物线解析式为y=2x2﹣4x﹣6.
,∴抛物线解析式为y=2x2﹣4x﹣6.
(2)y=2x﹣2,令x=0,y=﹣2,∴F(0,﹣2),由![]() 解得
解得![]() 或
或![]() ,∴点D坐标(2,﹣6).∵点C(0,﹣6),∴CD⊥CF,∴∠DCF=90°,由题意:P点移动的路程为DP=t,Q点移动的路程为3(t﹣1)=3t﹣3,当Q点在CD上时,即0<3t﹣3≤2时,1<t≤
,∴点D坐标(2,﹣6).∵点C(0,﹣6),∴CD⊥CF,∴∠DCF=90°,由题意:P点移动的路程为DP=t,Q点移动的路程为3(t﹣1)=3t﹣3,当Q点在CD上时,即0<3t﹣3≤2时,1<t≤![]() 时,如图1中,若PQ⊥DF,则有Rt△QDP∽Rt△FCD,
时,如图1中,若PQ⊥DF,则有Rt△QDP∽Rt△FCD,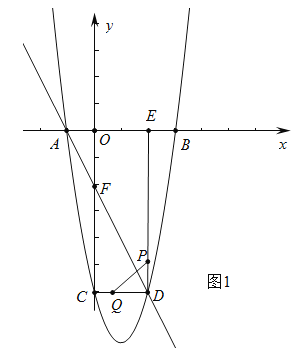
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴t=3,3>
,∴t=3,3>![]() ,∴此时t不合题意.
,∴此时t不合题意.
当点Q在CO上时,2<3t﹣3≤8,![]() <t≤
<t≤![]() 时,如图2中,过点P作PK⊥OC于K,
时,如图2中,过点P作PK⊥OC于K,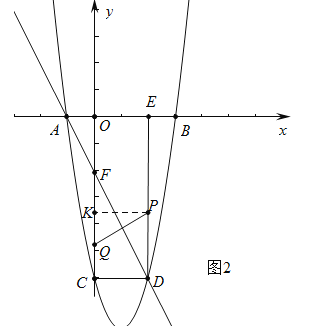
∴CK=PD=t,CQ=3(t﹣1)﹣2=3t﹣5,若PQ⊥DF,则有Rt△PKQ∽Rt△FCD,∴![]() ,即
,即![]() =
=![]() ,∴t=2.∵
,∴t=2.∵![]() <t≤
<t≤![]() ,∴t=2符合题意.
,∴t=2符合题意.
当点Q在OE上时,即8≤3t﹣3≤10,![]() ≤t≤
≤t≤![]() 时,如图3中,
时,如图3中,
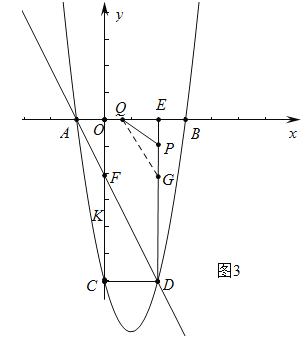
若PQ⊥DF,过点Q作QG∥DF交DE于G,则QG⊥QP,即∠GQP=90°,∴∠QPE>90°,这与△QPE内角和为180°矛盾,此时PQ不与DF垂直.
综上所述:当t=2时,有PQ⊥DF.
(3)分三种情况讨论:
①当∠MAB=45°且M在x轴上方时.∵A(-1,0)在y轴上取点P(0,1)直线AP交在线CB于M,则∠MAB=45°,如图4.易求直线AP为y=x+1,易求直线BC的解析式为:y=2x-6,解方程组:![]() ,解得:
,解得:![]() ,∴M(7,8);
,∴M(7,8);
②当∠MAB=45°且M在x轴下方时.在y轴上取点Q(0,-1)直线AQ交在线CB于M′,则∠M′AB=45°,类似可求M(![]() ,
,![]() );
);
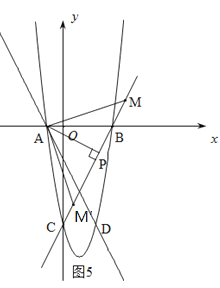
③若∠AMB=45°,过A作AP⊥BC于P,则△APM是等腰直角三角形,∴AP=PM.如图5.∵AP⊥CB,∴直线AP为![]() ,解方程组:
,解方程组: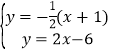 ,解得:
,解得: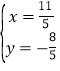 ,∴P(
,∴P(![]() ,
,![]() ),∴AP=
),∴AP=![]() =
=![]() .设M(a,2a-6),则MP=AP,∴
.设M(a,2a-6),则MP=AP,∴![]() =
=![]() ,整理得:25a2-110a+57=0,∴(5a-19)(5a-3)=0,解得:a=
,整理得:25a2-110a+57=0,∴(5a-19)(5a-3)=0,解得:a=![]() 或a=
或a=![]() ,∴M(
,∴M(![]() ,
,![]() )或M′(
)或M′(![]() ,
,![]() ).
).
综上所述:存在一个点M,使△ABM中有一个角为45°,M的坐标为:M(7,8)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF.
(1)求证:直线CA是⊙O的切线;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
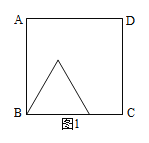
【题目】如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)当t=2时,点Q到BC的距离=_____;
(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;
(3)若点Q在AD边上时,如图2,求出t的值;
(4)直接写出点Q运动路线的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A,O,B,C,D分别表示-3,0,2.5,5,-6.
![]()
(1)求B,O两点间的距离;
(2)求A,D两点间的距离;
(3)求C,B两点间的距离;
(4)请观察思考,若点A表示数m,且m<0,点B表示数n,且n>0,用含m,n的代数式表示A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点D是正方形OABC的边AB上的动点,OC=6.以AD为一边在AB的右侧作正方形ADEF,连结BF交DE于P点.
(1)请直接写出点A、B的坐标;
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系?若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
(3)当P点为线段DE的三等分点时,试求出AF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
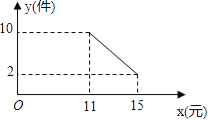
(1)求销售量y与定价x之间的函数关系式;
(2)如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
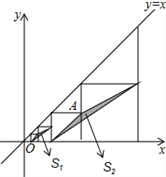
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个大正方形和四个全等的小正方形按图①、②两种方式摆放,设小正方形的边长为x,请仔细观察图形回答下列问题.
(1)用含a、b的代数式表示x,则x=____.
(2)用含a、b的代数式表示大正方形的边长____.(请将结果化为最简)
(3)利用前两问的结论求出图②的大正方形中未被小正方形覆盖部分的面积.(用a、b的代数式表示)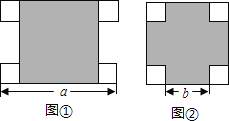
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)图(1)是一个长为2m,宽为2n的矩形,把此矩形沿图中虚线用剪刀均分为四个小长方形,然后按图(2)的形状拼成一个大正方形.请问:这两个图形的什么量不变?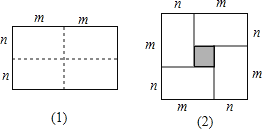
(2)把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m,n的代数式表示为(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的结论是:在周长一定的矩形中,当 时,面积最大.
(4)若矩形的周长为24cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com